波動関数（読み）ハドウカンスウ（英語表記）wave function

デジタル大辞泉

はどう‐かんすう〔‐クワンスウ〕【波動関数】

波動方程式を満足させる関数。量子力学では粒子の状態を表す関数をいい、この絶対値の2乗はその点に粒子の存在する確率密度を表す。

出典　小学館

精選版 日本国語大辞典

はどう‐かんすう‥クヮンスウ【波動関数】

1. 〘 名詞 〙 波動を表わす関数。古典力学では座標および時間を独立変数として媒質の変位を表わし、量子力学では電子などの物質粒子の状態を示す波動的な関数で、その二乗がその粒子の存在確率を表わす。〔自然科学的世界像（1938）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

波動関数
はどうかんすう
wave function

量子力学において、原子・分子および原子核・素粒子の状態を表すのに用いられる座標の関数のこと。状態関数ということもある。座標の関数のかわりに運動量その他の量（力学変数）の関数を用いることもある。座標の関数を運動量の関数に変換することができるので、どの力学変数を用いても波動関数の表す状態の物理的内容が変わることはない。

　原子や素粒子などの量子力学における運動状態を量子的状態という。量子力学では物理量は演算子で表現されており、物理量がある値をとる状態の波動関数はこの物理量の演算子の固有関数で与えられる。たとえばx方向の運動量の演算子は-iħ∂/∂x（ħはプランク定数hの2π分の1）であるので、固有値p'の波動関数∅(x)は固有値方程式-iħ∂∅(x)/∂x=p'∅(x)を満たし、波動関数は∅(x)=c exp(ip'x/ħ)で与えられる。ただし、expα=e^αを表す。cはそれぞれの場合の物理的条件に応じて決まる定数である。波動関数の時間的変化は系のエネルギーの演算子Hを用いiħ∂/∂t=Hで与えられる。これをシュレーディンガーの波動方程式とよんでいる。この系が固有値Eのエネルギーの固有状態であればH=Eであって、この場合の波動関数の時間変化は=∅exp(iEt/ħ)となる。ここで∅は時間によらないH∅=E∅を満たす波動関数である。この方程式もシュレーディンガー方程式という。

［田中　一］

[参照項目] | シュレーディンガーの波動方程式 | プランク定数 | 量子力学

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

波動関数 (はどうかんすう)
wave function

広い意味では波動現象を記述する関数をいうが，量子力学（波動力学）におけるものを指すことが多い。波動力学では，電子，光子などの微粒子は粒子的性質と波動的性質の両方をもっていて，そのふるまいは波動関数ψ（x，y，z，t）によって表されると考える。ψ（x，y，z，t）は波動方程式（シュレーディンガー方程式）に従い，粒子の種類やその粒子がどのような条件の下におかれているかによって定まる。そして，この場合のψ（x，y，z，t）は抽象的空間における複素関数であり，

　｜ψ（x，y，z，t）｜²dxdydz

は，ある時刻tにその粒子が点（x，y，z）を含む微小な体積dxdydz内に見いだされる確率を与えると解釈されている。
→波動力学
執筆者：有山 正孝

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

波動関数
はどうかんすう
wave function

一般には波の振幅を表わす関数をいうが，狭義には量子力学において確率振幅を表わす関数 Ψ をさす。 Ψ は電子などの状態を記述するため，状態関数とも呼ばれる。 Ψ は電子の位置座標 r と時間 t の関数であり，Ψ の時間的変化はシュレーディンガーの波動方程式によって規定され，適当な境界条件のもとで解くことによって決定される。 Ψ そのものは観測可能な量ではないが，｜Ψ｜²dτ は時刻 t に電子が r の位置で微小体積 dτ のなかに見出される確率を与える。

出典　ブリタニカ国際大百科事典 小項目事典

化学辞典 第2版

波動関数
ハドウカンスウ
wave function

一般には，波の動きを表現する時間と空間の関数．しかし，量子力学の一形式である波動力学が出現してからは，対象となる系の量子状態を表す状態関数と同意義に使われている．波動関数の絶対値の2乗は，対象としている系の状態のその空間と時間に存在する確率に比例する．

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内の波動関数の言及

【原子】より

…この場合は，電子雲の各部分と陽子との間の距離がそれぞれ異なるので，古典力学(ニュートン力学)との類似性が希薄になる。このような場合を含めて，一般に電子の状態は一つの波動関数ψ(x,y,z,t)で表される(x,y,zは位置座標)。管の中で空気を振動させると定常波が生ずることがあるが，量子力学によれば，原子内の電子の波についても定常波があり，定常波が存在するときその状態を定常状態と呼ぶ。…

【波動力学】より

…x_iと時間tの関数ψ(x_i,t)に対する微分方程式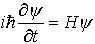，がシュレーディンガーの波動方程式である。波動関数がψ(x,t)＝exp(－iEt/ħ)φ(x)の形のものを定常状態と呼び，方程式は固有値問題，　Hφ＝Eφとなる。これもシュレーディンガー方程式と呼ばれる。…

【量子力学】より

…同様に，量子力学においても，運動を表現する波動に対して，一時刻tにおけるその形から以後の移りゆきを完全に決める方程式があり，それを提出した人の名をとってシュレーディンガーの波動方程式とよばれる。空間の各点における波動の値(複素数)をあたえる関数は波動関数とよばれる。波動方程式は波動関数に対する偏微分方程式である。…

※「波動関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」