スティルチェス積分（読み）スティルチェスせきぶん（英語表記）Stieltjes integral

改訂新版　世界大百科事典

スティルチェス積分 (スティルチェスせきぶん)
Stieltjes integral

スティルチェスT.J.Stieltjes（1856-94）がリーマン積分の拡張として定義した積分である。区間a≦x≦bで有界な関数f（x），g（x）があるとき，リーマン積分の場合と同様な近似和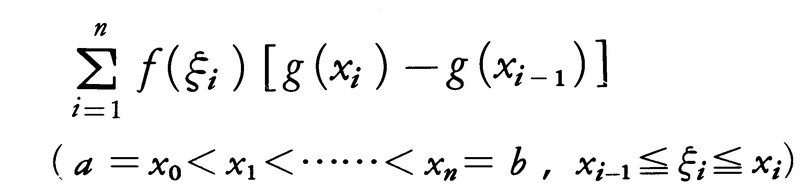

を作る。分割を一様に細かくしていくとき，この近似和が一定の値に近づく場合に，その値をf（x）のg（x）に関するスティルチェス積分，詳しくはリーマン=スティルチェス積分といい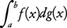，と書く。g（x）＝xの場合がふつうのリーマン積分である。f（x），g（x）の一方が有界変動，他方が連続ならばリーマン=スティルチェス積分が存在する。またそのとき，部分積分法の公式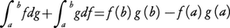，が成立する。とくにg（x）の導関数g′（x）が存在して連続ならば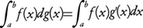，が成立する。
→積分
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

スティルチェス積分
スティルチェスせきぶん
Stieltjes integral

f(x) および g(x) を閉区間 [a，b] で定義された有界な関数とし，[a，b] の分割 Δ を，a＝x₀＜x₁＜x₂＜x₃＜…＜x_n＝b とする。この分割 Δ に対し，[x_i，x_i-1] に含まれる任意の点 t_i を選んで，和
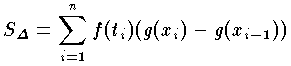をつくる。分割 Δ の幅のうちで最大のもの，すなわち δ＝ max (x_i－x_i-1) を限りなく0に近づけるとき，あらゆる分割の仕方，およびそれに応じる t_i のとり方にかかわらず S_Δ が一定の極限値に収束するならば，その極限値を
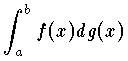と書き，関数 g(x) を用いてつくられる f(x) のスティルチェス積分という。

出典　ブリタニカ国際大百科事典 小項目事典