日本大百科全書(ニッポニカ) 「フィボナッチ数列」の意味・わかりやすい解説
フィボナッチ数列
ふぃぼなっちすうれつ
初項と第2項を1とし、第3項以後次々に前2項の和をとって得られる数列。つまり、
a1=1, a2=1, an+1=an+an-1
(n=2, 3, 4,……)
で表され、
1, 1, 2, 3, 5, 8, 13, 21, 34,……
という数列となる。これはフィボナッチが『算術の書』(1202)のなかで、次のような問題として提起したものである。「一つがいのウサギは、生まれて2か月後から、毎月一つがいの子供を産むとする。初めの生まれたての一つがいがいるとき、1か月後、2か月後、……のウサギのつがいの総数を求めよ」。
フィボナッチ数列の相隣る項の比をとってできる数列a2/a1, a3/a2,……つまり、
1, 2, 5/3, 8/5,……
は、無限連分数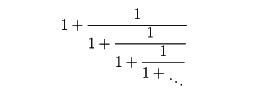
を途中で打ち切って得られる分数の列である。この分数列は (1+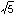 )/2 に収束する。この極限値は、黄金比(黄金分割の比)として、古来、重要視された数である。anは、
)/2 に収束する。この極限値は、黄金比(黄金分割の比)として、古来、重要視された数である。anは、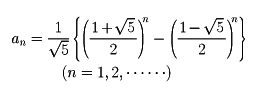
と表すことができる。
[竹之内脩]
占い用語集 「フィボナッチ数列」の解説
フィボナッチ数列
出典 占い学校 アカデメイア・カレッジ占い用語集について 情報
世界大百科事典(旧版)内のフィボナッチ数列の言及
【黄金分割】より
…正五角形の同じ頂点を通らない2本の対角線は互いに他を黄金分割する(図3)。1,1よりはじめて順次に前の2項の和をつくることによって得られる数列 1,1,2,3,5,8,13,……をフィボナッチ数列というが,この数列より相隣る2項の比をつくることによって得られる分数の数列 1/1,1/2,2/3,3/5,5/8,8/13,……は黄金比に近づく。黄金比は連分数により次のように表される。…
【建築モデュール】より
…単位は10cmまたは4インチであり,10cmの場合は1を10とし,4インチの場合は1を4として数列を読みかえる。 フィボナッチ数列は直前2項の和を次の項とする数列であり,並び合う2項の比が急速に黄金比に収束するため,建築においては特殊な意味をもたされている数列である。この数列ではその定義により,ある制限内でのモデュールの合成や分解は可能であるが,寸法の割込みなどには不つごうであるため,多くは他の倍数系列と組み合わせて使われる。…
※「フィボナッチ数列」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...

