黄金分割（読み）オウゴンブンカツ

デジタル大辞泉

おうごん‐ぶんかつ〔ワウゴン‐〕【黄金分割】

線分を黄金比に分けること。外中比分割。中外比分割。

出典　小学館

精選版 日本国語大辞典

おうごん‐ぶんかつ ワウゴン‥【黄金分割】

〘名〙 線分を黄金比に分けること。外中比分割。中末比分割。中外比分割。黄金截(おうごんせつ)。〔音引正解近代新用語辞典（1928）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

黄金分割
おうごんぶんかつ

線分を黄金比に分けること。黄金比とは、ある長方形の2辺の長さの比で、その長方形から短い辺を1辺とする正方形を除いてできる残りの長方形が初めの長方形と相似になるものである。図Aのように、長方形ABCDと正方形ABB'A'をとる。長方形ABCDと、長方形A'B'CDが相似であるなら、B'は線分BCを黄金分割する。いま、長方形ABCDの1辺ABの長さを1とし、ADの長さをxとすれば、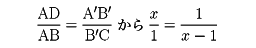

xに関する二次方程式x²－x－1＝0を解いて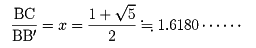

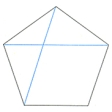
したがって黄金比の値はだいたい1.618である。正五角形の1辺と対角線の長さの比は黄金比になっている。また、正五角形の一つの対角線は、他の一つの対角線によって黄金比に分けられている（図B）。

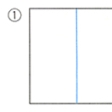
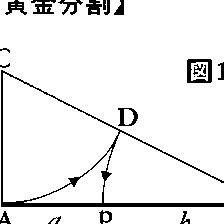
　一つの線分の黄金分割を作図で求めるには次のようにすればよい。まず、その線分の一端で半分の長さの垂線を立て直角三角形をつくる。次に、その斜辺から初めの線分の半分を除いた残りの長さを初めの線分上にとる。これで黄金分割が完成する（図C）。また、黄金比をもつ長方形を作図するには次のようにすればよい。一つの正方形をとり、それを対辺の中点を結んで二つの長方形に分ける。その長方形の対角線の長さだけ正方形の辺の中点から辺を延長すれば完成する（図D）。

［柴田敏男］

黄金比とフィボナッチ数列

フィボナッチ数列とは、初項と第2項が1で、第3項以降次々と前2項の和をとってつくられる数列である。

　　1，1，2，3，5，8，13，21，……
がそれである。このフィボナッチ数列の相隣る項の比をとってできる数列、すなわち
　　1，2，3/2，5/3，8/5，13/8，……
の極限値は黄金比と等しい。しかもこの数列の第5項以降の小数第1位までをとると、すべて1.6で、黄金比1.618……とほぼ等しい。

　松かさを手にとって観察すると、右巻きと左巻きの二つの渦巻が交錯しているのがみられるが、その筋の個数は8本と5本になっている。8と5はフィボナッチの数列の1組の相隣る項である。パイナップルの実や菊の花のなかにも二つの交錯する渦があり、その筋の個数はそれぞれ13対8、34対21となっている。これもフィボナッチ数列の相隣る項の比である。黄金比1.6は自然の神秘のなかにも現れているといえる。

　黄金比をもつ長方形はもっとも調和のとれた長方形といわれている。古代ギリシアの建造物や美術・工芸品には、黄金比や黄金比長方形に近似する比や形をもつものがしばしば見受けられる。たとえば、アテネのパルテノン神殿の輪郭は黄金比長方形に近い。また、ルネサンス期イタリアの万能人であったレオナルド・ダ・ビンチは黄金比の長方形を活用して絵を描いたともいわれている。

［柴田敏男］

『マイケル・ホルト著、西田稔訳『芸術における数学』（1976・紀伊國屋書店）』▽『ヘルマン・ヴァイル著、遠山啓訳『シンメトリー』（1957・紀伊國屋書店）』

[参照項目] | フィボナッチ数列

黄金分割〔図A〕

黄金分割〔図B〕

黄金分割〔図C〕

黄金分割〔図D〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

黄金分割
おうごんぶんかつ
golden section; Golden Mean system of proportion

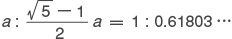線分を二つの部分に分割するとき，線分全体の長さと大きな部分の長さの比が，大きな部分と小さな部分の長さの比と等しくなるようにすること。すなわち線分 AB上に点 Pがあり，AB：AP＝AP：PB，または AB×PB＝AP² であるとき，この点 Pによる線分 ABの分割を黄金分割と呼ぶ。また，線分の長さを a とした場合の を黄金比という。前5世紀中頃にギリシアで発見されて以来，調和的で美しい比例関係を生み出すものとして重んじられ，パルテノンをはじめとするギリシア建築に採用された。またローマ時代にもウィトルウィウスが『建築十書』De Architectura（前25頃）でこれを取り上げ，中世の建築家たちもしばしば黄金比を採用している。ルネサンス期にはボローニャの修道士ルカ・パチオーリが「神聖比例」と名づけ，『神聖比例論』De divina proportione（1509，挿絵はレオナルド・ダ・ビンチ）において詳論している。19世紀のドイツの美学者アドルフ・ツァイジングやグスタフ・テオドール・フェヒナーの研究によれば，黄金比は優れた作品の構図や建築に，しばしば意識的，無意識的に採用されているほか，自然界，たとえば葉脈，種子の形状，貝殻の渦，細胞の成長などにも見られるという。近代絵画や近代建築においても，キュビスムや抽象主義派などによって探求の対象となっている。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

黄金分割 (おうごんぶんかつ)
golden section

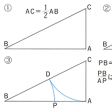
線分AB上に1点PをとってAP・AB＝PB²となるように分けることを黄金分割といい，このときの比AP：PBを黄金比という。古代ギリシアでは縦横の長さがこの比をなす長方形がもっとも形がよいとされたので，このように呼ばれてきた。黄金比は（\(\sqrt{5}\)－1）/2＝0.61803……で，ABを黄金分割する点Pを求めるには次のようにすればよい。AにおいてABに立てた垂線上に点CをAC＝1/2ABとなるようにとり，次にCB上に点DをCD＝CAとなるようにとり，さらにAB上に点PをBP＝BDとなるようにとる（図1）。半径bの円に内接する正十角形の1辺の長さをaとするとき，a：bは黄金比となる（図2）。正五角形の同じ頂点を通らない2本の対角線は互いに他を黄金分割する（図3）。1，1よりはじめて順次に前の2項の和をつくることによって得られる数列1，1，2，3，5，8，13，……をフィボナッチ数列というが，この数列より相隣る2項の比をつくることによって得られる分数の数列1/1，1/2，2/3，3/5，5/8，8/13，……は黄金比に近づく。黄金比は連分数により次のように表される。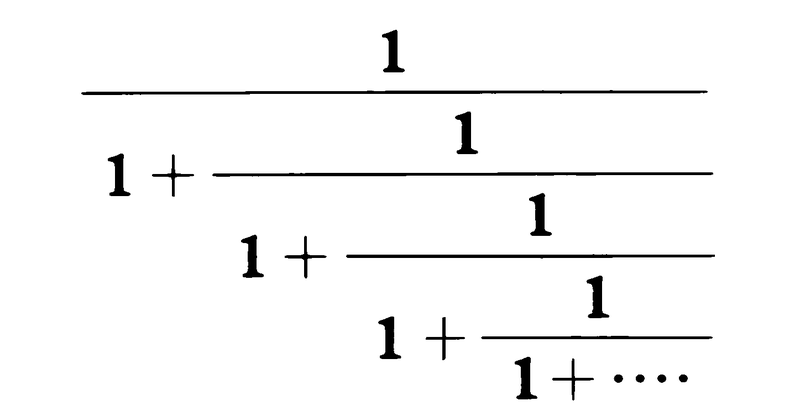

上記の分数の数列はこれの近似分数である。黄金分割はもっとも調和のある美しい分割法として，この比は優れた美術作品や建築にしばしば意識的，もしくは無意識的に採用されている。また，黄金比と近似する上記の分数の数列は種子の配列，貝殻の渦の成長など，自然界にしばしば見られる。
執筆者：中岡 稔

図－黄金分割

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

黄金分割【おうごんぶんかつ】

線分ABを点Pで分割し，BP/AP＝AP/AB，つまりAP²＝BP・ABとすること。（式１）または（式２）となり，これを黄金比という。黄金比はギリシア時代から最も調和のとれた比といわれ，絵画，建築等に応用され，本やはがきの縦横比もこれに近い。

出典　株式会社平凡社