日本大百科全書(ニッポニカ) 「二次方程式」の意味・わかりやすい解説
二次方程式
にじほうていしき
二次の代数(整)方程式を二次方程式という。一般形はxを未知数として
ax2+bx+c=0 (a≠0)
で表される。これは正確にいえば未知数が一つであるから一元二次方程式である。二次方程式ax2+bx+c=0の解法は最初の2項を用いて完全平方式をつくり、開平して解(根(こん))の公式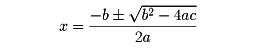
が得られる。この公式に現れるb2-4acを方程式の判別式という。実数係数の場合、この判別式が正の値をとるときは二根とも実数(実根)であり、負の値をとるときは複素数(虚根)であり、また判別式の値がゼロのときは二根は等しい(等根または重根)。この場合、係数が複素数でも重根である。根の公式から、二根をα、βとすると、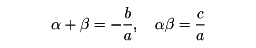
が得られる(根と係数との関係)。
四次方程式
a(px2+qx+r)2+b(px2+qx+r)+c=0
は括弧(かっこ)内の二次式をXと置くと、Xについての二次方程式となるから、xの複二次方程式とよばれる。Xについて解き、二根のα、βが得られれば、次に二つの二次方程式
px2+qx+r=α, px2+qx+r=β
を解いて、一般に四根を得る。
未知数x、yについての二元二次方程式を連立して、一般形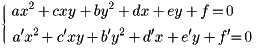
の連立二元二次方程式を得る。係数が実数のとき、この解の幾何学的意味は、各方程式はそれぞれ二次曲線(円、楕円(だえん)、放物線、双曲線および二直線)を表すから、二つの二次曲線の交点の座標である。
[竹内芳男]
《モスクワに遠征したナポレオンが、冬の寒さと雪が原因で敗れたところから》冬の厳しい寒さをいう語。また、寒くて厳しい冬のこと。「冬将軍の訪れ」《季 冬》...
1/16 デジタル大辞泉プラスを更新
1/16 デジタル大辞泉を更新
12/10 小学館の図鑑NEO[新版]魚を追加
10/17 ブリタニカ国際大百科事典 小項目事典を更新
8/22 日本大百科全書(ニッポニカ)を更新

