全微分 (ぜんびぶん)
total differential
2変数の関数z=f(x,y)が点(x,y)において偏微分可能であって,
f(x+h,y+k)-f(x,y)=hf(x,y)+kfy(x,y)+εy(h,k)
とおくとき,εy(h,k)/(|h|+|k|)→0(|h|+|k|→0)となるならば,f(x,y)は(x,y)において全微分可能であるといい,
dz=f(x,y)dx+fy(x,y)dy
と書いて,これをz=f(x,y)の(x,y)における全微分という。f(x,y)が偏微分可能でも全微分可能とは限らないが,偏微分可能でかつ偏導関数の一方が連続な点では,全微分可能であることが示される。
f(x,y)が全微分可能であって,f(x,y),fy(x,y)も全微分可能ならば,fy=fyとなる。このときzの第2階全微分が,
d2z=d(dz)=(fdx+fydy)dx+(fdx+fydy)ydy=fdx2+2fydxdy+fyydy2
によって定義される。一般にz=f(x,y)の第m-1階までの偏導関数が全微分可能なとき,zの第m階全微分は,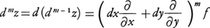 によって定義される。ここでfに対する偏微分演算は上式の
によって定義される。ここでfに対する偏微分演算は上式の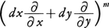 を二項定理で形式的に展開したものを施したものと解する。
を二項定理で形式的に展開したものを施したものと解する。
一般のn変数の関数z=f(x1,x2,……,xn)の第m階全微分も,上と同様に考えて,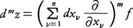 と定義する。
と定義する。
→偏微分
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
全微分
ぜんびぶん
変数を微小に変化させたときの多変数関数の関数値の微小変化を表すことば。一変数の関数f(x)では、ある点x=x0においてf(x)が微分可能ならば、それは、
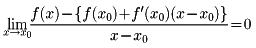
であることを意味する。同様のことを多変数の関数で考える。以下、二変数の場合について説明する。z=f(x,y)は、点P0(x0,y0)の近くで定義された関数であるとき、適当な定数A、Bがあって、
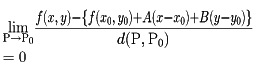
となるとき、f(x,y)はP0(x0,y0)で全微分可能であるという。ここで
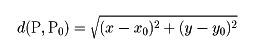
とする。このことは、点P(x,y)がP0(x0,y0)に十分近ければ、f(x,y)-f(x0,y0)は近似的にA(x-x0)+B(y-y0)であることをいっている。ここで
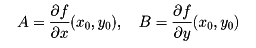
となるので、このことを
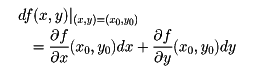
または
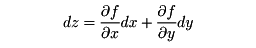
と表し、これをzの全微分という。f(x,y)がC1級関数(連続な偏導関数を有する関数)のときは全微分可能であるが、単にx、yの双方について偏微分可能というだけでは、全微分可能とはならない。全微分は、関数値を近似的に計算するための意味をもつが、そのほか、数理科学の理論の基礎として重要な概念である。たとえば数理経済学において、物価vが、いくつかの要因x1,x2,……,xnの関数v(x1,x2,……,xn)であるとき、要因の変動Δx1,Δx2,……,Δxnに基づく物価の変動Δvは、
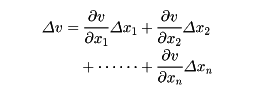
で表される。
[竹之内脩]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
全微分
ぜんびぶん
total differential
2変数の関数 Z=f(x,y) が,閉区間
U={a-δ≦x≦a+δ,b-δ≦y≦b+δ}
で偏導関数 fx(x,y) ,fy(x,y) をもち,これらの偏導関数が点 (a,b) において連続とする。 c=f(a,b) ,x=a+h ,y=b+k とするとき変数が (a,b) から (x,y) まで変動した場合の関数値の変動量 z-c=f(x,y)-f(a,b) は,z-c=h・fx(a,b)+k・fy(a,b)+ε で与えられる。この右辺の h・fx(a,b)+k・fy(a,b) を点 (a,b) における,変動 (h,k) に対する z=f(x,y) の全微分あるいは単に微分といい,dz と書く。特に x を f(x,y) の関数,y を f(x,y) の関数と考えれば,h=dx ,k=dy となるから,全微分は,dz=fx(a,b)dx+fy(a,b)dy で表わすことができる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
全微分【ぜんびぶん】
2変数x,yの関数f(x,y)が一点(a,b)で偏微分可能で,f(a+h,b+k)−f(a,b)=hf(/x)(a,b)+kf(/y)(a,b)+ε(h,k)とおいたとき,h→0の極限で(式1)となるならば,f(x,y)は(a,b)で全微分可能であるという。f(x,y)が全微分可能なら連続でしかも偏微分可能である。しかしf(x,y)が全微分可能であるためには,偏微分可能であるほかに,偏導関数が連続であることが必要。この場合(式2)と書き,これをf(x,y)の全微分という。3個以上の変数(x1,x2,…,x(/n))の関数f(x1,x2,…,x(/n))についても同様で,全微分(式3)が定義される。→微分/偏微分
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内の全微分の言及
【微分】より
…このときzをtで微分する公式は,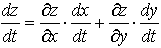 で与えられる。
で与えられる。
【全微分】
関数z=f(x,y)の定義域の中に1点(a,b)をとり,そこから変数をそれぞれ⊿x,⊿yだけ変化させたとき,点(a,b)と点(a+⊿x,b+⊿y)との距離ρは,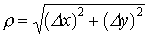 であり,そのとき関数の値zの変化は, ⊿z=f(a+⊿x,b+⊿y)-f(a,b)である。fx,fyがともに連続ならば, ⊿z=fx(a,b)⊿x+fy(a,b)⊿y +ε(⊿x,⊿y)・ρ ……(16) とおくと,ρ→0のときε(⊿x,⊿y)→0となる。…
であり,そのとき関数の値zの変化は, ⊿z=f(a+⊿x,b+⊿y)-f(a,b)である。fx,fyがともに連続ならば, ⊿z=fx(a,b)⊿x+fy(a,b)⊿y +ε(⊿x,⊿y)・ρ ……(16) とおくと,ρ→0のときε(⊿x,⊿y)→0となる。…
※「全微分」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
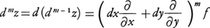 によって定義される。ここでfに対する偏微分演算は上式の
によって定義される。ここでfに対する偏微分演算は上式の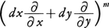 を二項定理で形式的に展開したものを施したものと解する。
を二項定理で形式的に展開したものを施したものと解する。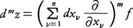 と定義する。
と定義する。

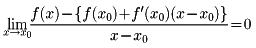
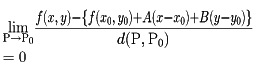
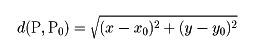
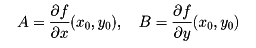
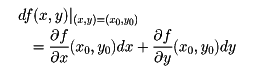
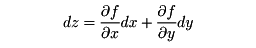
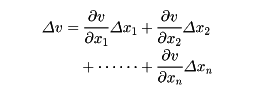
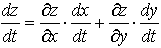 で与えられる。
で与えられる。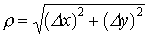 であり,そのとき関数の値zの変化は, ⊿z=f(a+⊿x,b+⊿y)-f(a,b)である。fx,fyがともに連続ならば, ⊿z=fx(a,b)⊿x+fy(a,b)⊿y +ε(⊿x,⊿y)・ρ ……(16) とおくと,ρ→0のときε(⊿x,⊿y)→0となる。…
であり,そのとき関数の値zの変化は, ⊿z=f(a+⊿x,b+⊿y)-f(a,b)である。fx,fyがともに連続ならば, ⊿z=fx(a,b)⊿x+fy(a,b)⊿y +ε(⊿x,⊿y)・ρ ……(16) とおくと,ρ→0のときε(⊿x,⊿y)→0となる。…