偏微分（読み）ヘンビブン（英語表記）partial differential

デジタル大辞泉

へん‐びぶん【偏微分】

偏導関数の一つの変数のみを変化させて関数の変化率を求めること。また、その値。

出典　小学館

精選版 日本国語大辞典

へん‐びぶん【偏微分】

〘名〙 多変数関数の偏導関数を求めること。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

偏微分 (へんびぶん)
partial differential

二つ以上の変数x，y，……の関数fがあるとき，これを一つの変数，例えばxだけに注目し，他の変数は固定して定数とみなし，xの関数として微分することを関数fをxで偏微分するという。関数fをxで偏微分することによって得られる微分係数を変数xに関するfの偏微分係数と呼んで，\(\frac{∂f}{∂x}\)，またはf_xと書く。例えば2変数の関数f（x，y）について書くと，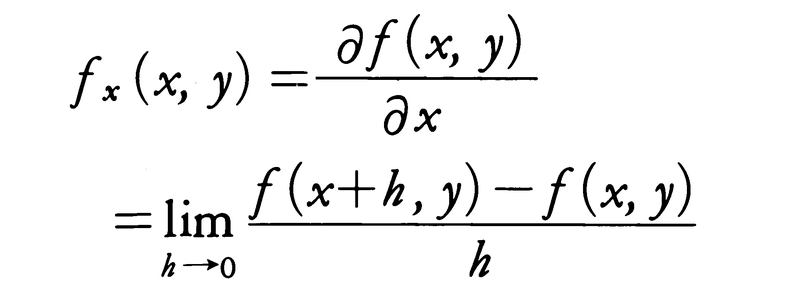

がfのxに関する偏微分係数である。これをx，yの関数と考えるときfのxに関する偏導関数という。偏微分係数，あるいは偏導関数を求める手続を偏微分法というが，この偏微分法のことを偏微分と略称することが多い。むしろこの略称のほうがふつうに使われているので，検索の便宜のため偏微分を項目名とした。なお，偏導関数のことを偏微分と呼ぶことがあるが，これは正しい用法ではない。上に述べた\(\frac{∂f}{∂x}\)の定義と同様にして，xを固定してyについて微分することにより，変数yに関するfの偏導関数が定義される。さらに高階の偏導関数の定義や性質などについては，〈微分〉の項を見られたい。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

偏微分【へんびぶん】

n個の変数x₁，x₂，…，x(/n)の関数f（x₁，x₂，…，x(/n)）があるとき，変数のうちの一つ，たとえばx(/i)を除いた他のn−１個の変数の値を固定し，これによって生じるx(/i)だけの関数をx(/i)について微分することを，関数fをx(/i)で偏微分するという。これによって得られる微分係数，導関数をx(/i)に関する偏微分係数，偏導関数といい，∂f/∂x(/i)または（式１）と書く。一点またはある範囲で，ある関数のすべての変数に関する偏微分係数が存在するとき，その関数はその点または範囲で偏微分可能であるという。→微分／全微分
→関連項目コワレフスカヤ

出典　株式会社平凡社