双曲幾何学（読み）そうきょくきかがく

日本大百科全書(ニッポニカ)

双曲幾何学
そうきょくきかがく

ユークリッド幾何学の公理系のなかの平行線公理を「平面上で直線外の1点を通ってこの直線と交わらない直線が少なくとも2本存在する」で置き換えて得られる幾何学を、双曲幾何学またはロバチェフスキーの幾何学という。この幾何学は1820年代にN・ロバチェフスキーとJ・ボヤイによって提唱された。

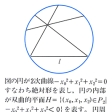
　射影幾何学は射影平面P₂とそれに作用する射影変換群によって決まる古典幾何学（クラインの幾何学）であるが、P₂の二次曲線
　　-x₀²+x₁²+x₂²=0
を不変にする部分群がP₂の部分集合
　　H=｛(x₀,x₁,x₂)
　　　∈P₂|-x₀²+x₁²+x₂²＜0｝
に作用することによって決まる古典幾何学が双曲幾何学である。このとき二次曲線
　　-x₀²+x₁²+x₂²=0
を絶対形といい、Hを双曲的平面という。Hの二直線は絶対形の上で交わるとき平行であるといわれる。直線l外の1点を通ってlに平行な直線が2本存在し、lに交わらない直線は無数に存在する。

　現代的な見地では双曲幾何学は負の定曲率空間上のリーマン幾何学にほかならない。単位円板｛（x,y）∈R²｜x²+y²＜1｝にリーマン計量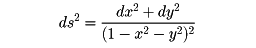

を与えて得られるリーマン幾何学や、上半平面｛（x,y）∈R²｜y＞0｝にリーマン計量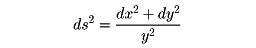

を与えて得られるリーマン幾何学がそのモデルである（ポアンカレ・モデル）。これらのモデルでは直線すなわち測地線は円周およびx軸に直交する円または直線である。一般にn次元の双曲幾何学が二次元の場合とまったく同様に考えられる。

［荻上紘一］

[参照項目] | 平行線公理

双曲幾何学（絶対形と双曲的平面）

双曲幾何学（リーマン幾何学）

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の双曲幾何学の言及

【幾何学】より

…なお，B.リーマンは1854年に，直線の長さは有限で，2直線はつねに2点で交わるような幾何学を構成し，クラインはこれを少しく変更して2直線はつねに1点で交わるという幾何学を構成した。この非ユークリッド幾何学を楕円幾何学と呼ぶのに対し，先に述べた非ユークリッド幾何学を双曲幾何学と呼ぶ。三角形の内角の和は楕円幾何学では2直角より大きく，双曲幾何学では2直角より小さい。…

【非ユークリッド幾何学】より

…さらに，直線は有限で閉じたものとなり，直線上の点の間の順序についてもユークリッド幾何学の場合と相違する性質がみられる。先に述べた非ユークリッド幾何学を双曲幾何学と呼び，この幾何学を楕円幾何学という。これらに対応してユークリッド幾何学は放物幾何学と呼ばれる。…

※「双曲幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」