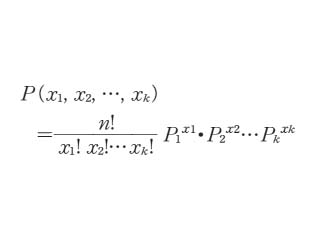改訂新版 世界大百科事典 「多項分布」の意味・わかりやすい解説
多項分布 (たこうぶんぷ)
multinomial distribution
これは二項分布の一般化と見られる多次元格子点上の離散型確率分布である。毎回独立に同じ試行を繰り返すとき,各試行でr個の実現可能性がある場合(それぞれ事象E1,E2,……,Erとする)を対象とする。各試行でそれらが起こる確率をp1,p2,……,pr(ただしp1+p2+……+pr=1である)とすれば,n回の試行のうちE1がk1回,E2がk2回,……,Erがkr回起こる確率は,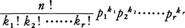
で与えられる。ここで各kiは0または正の整数で,k1+k2+……+kr=nを満たす。上記確率は(p1+p2+……+pr)nの展開の一般項を表しているので多項分布と呼ばれる。この分布は数理統計学における標本の任意抽出法で母集団がr個に類別されている場合,返却を許す標本抽出法に応用される。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


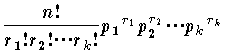 になる。これを多項分布という。これはちょうど (p1+p2+…+pk)n を
になる。これを多項分布という。これはちょうど (p1+p2+…+pk)n を