数理統計学（読み）スウリトウケイガク（英語表記）mathematical statistics

デジタル大辞泉

すうり‐とうけいがく【数理統計学】

統計学の数学的側面について研究する応用数学の一分野。観察対象となる母集団の統計的性質を記述する記述統計学と、母集団から抽出した標本から確率論に基づいて母集団の状態を推測する推計学に大別される。

出典　小学館

精選版 日本国語大辞典

すうり‐とうけいがく【数理統計学】

1. 〘 名詞 〙 ＝すいけいがく（推計学）〔推計学の話（1949）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

数理統計学 (すうりとうけいがく)
mathematical statistics

統計学はもともとヨーロッパでおこり，国勢調査や税収の状況，あるいは貿易の量など国家の重要事項に関するデータの集りの取扱いを意味しており，今日のものとは異なる意味をもつものであった。その後，多数の数値を扱う数学的理論が開発されるに従って，数理統計学として応用数学の一分野にまで発展するに至った。それは，（1）データのもとになる集団に対する研究，（2）集団の変動の研究，（3）データの分布状況の特性を見いだすことなどを目標とする。すなわち，その目的は個々のものに関する興味にあるのではなくて，すべての個体をひとまとめにした集団の特性を論ずることにある。ここで集団という概念は，単に物質的なものだけに限られてはいない。一つの量の観測を限りなく繰り返せば，その記録は測定値の集団と考えられる。これら集団が数量的に記述されているとして，それらをなんらかの確率的法則性に従う現象の一つの実現であるとみなすことによって，そのような数値の集合を解析するのが数理統計学である。このとき，想定された確率的法則性を確率モデルと呼ぶ。数理統計学の手法を有効に適用するためには，第1にモデルの選定が適切でなければならない。例えば，成功か失敗かのいずれかしかない試行を繰り返すとき，毎回独立な試行とみればいわゆるベルヌーイ試行がモデルとなる。そしてこのモデルに二項分布が対応する。しかし，データとして試行の結果だけを知った場合，二項分布を定めるパラメーターp，すなわち成功する確率を完全にいいあてることはできない。この例のように，一般にモデルから理論的に導かれる確率分布は未知のパラメーターを含む。それを母数と呼ぶ。与えられたデータからこの未知母数についての推論を行うことを統計的推論という。上のベルヌーイ試行の例でいえば，全試行の中で成功した回数をみて，pの値をよりよく推定することが統計的推論である。確率論の発展はこの推論の方法に大きな影響を与えてきた。

数理統計学の始まり

C.F.ガウスとP.S.ラプラスは，すでに19世紀の初めに母数の推定法を論じている。ラプラスは，その研究において，母数の真の値θと推定値θ＾との誤差を評価するのに絶対値｜θ－θ＾｜の単調関数を用いた。ガウスは誤差を（θ－θ＾）²として最良の推定値を求めるのがより自然であると主張し，天文観測の膨大な資料と偶然性の洞察から最小二乗法を確立して大きな成功をおさめた。ガウスはまた誤差の分布が正規分布となることを理論的に証明し，分布の型を決める典型的な方法を示した。さらに分散や高次モーメントをはじめ，今日の数理統計学の基礎となるいくつかの概念を導入し，その役割を明らかにした。これらラプラスやガウスの研究には，1763年に公にされたベイズの定理が支えになっており，原因から結果の生ずる確率があらかじめわかっているとき，原因の先験的な確率（事前確率）が与えられたら，結果が知られた後での原因の確率（事後確率）が計算できるという立場をとっている。この立場の理解については，後世まで議論されるところとなった。

記述統計学

一方，実用面からの要請で，多数のデータを統計的に扱う記述統計学の手法が開発された。なかでも有名なのはベルギーの学者L.A.J.ケトレの貢献である。彼はヨーロッパのあちこちに散らばった地点で，天文学，測地学および気象学的な同時観測を始めた。また国勢調査を手がけたり，第1回の国際統計学会を組織するなど統計学の多方面で活躍した。彼のもっていた〈平均人〉という概念は，人々のもつ各種の標識の測定値が正規分布に従って平均値のまわりに分布すると考え，その平均値をもつものを指していた。そのような考え方は母集団の概念を導入するうえで役だったのである。続いて，優生学の研究の創始者として知られるイギリスの科学者F.ゴールトンが現れ，人体測定研究所で調査した多数のデータを解説するために相関係数の概念を導入して統計学の新しい手法を開発した。これは回帰分析の方法に対して，先駆的な役割を果たすものとなった。その後現れた同じくイギリスの数学者K.ピアソンも，相関と回帰の理論をより数学的に発展させ，それを計量生物学に応用した。こうした人たちの努力で20世紀の初めになって，多数の資料を整理してその分布を得，分布の代表値としての平均値や分散を求め，さらにグループ間の相関係数によって相互関係を調べる記述統計学は一応まとまった学問体系となった。記述統計学の基礎概念は次のようなものである。

統計原表

統計の出発点となるものであって，例えばある年度の新成人男子の各人について身長，体重，視力などの数値を書きこんだものを指す。視力は小数点以下1位までの離散的な測定値である。身長，体重は本来連続量であるが，測定値としては適当に段階をつけて離散量にして統計原表に記入される。それらの数値の集団はそのままではあまりに膨大で，集団の性質がはっきりしない。そのために原表を整理し，集団としての性質を知りやすくするため，分布を求めたり特性量を計算したりする。

分布

上の新成人の身長の例でいえば，測定値を10cmごとの区間で組分けして，各組に属する人数の全体に対する割合を（例えば%で）表示する級分布と，身長が140cm以下，150cm以下，160cm以下，……の割合を表示する累加分布とがあり，両者を総称して分布という。これをさらに統計グラフに表すことができればいっそう見やすいものとなる。以上は1種類の測定値についての分布であるが，2種類，例えば身長と体重の両方を分布にしてみることもできる。それには，平面上に縦軸と横軸をとって，一方の軸に身長の測定値を，他方に体重をとり，身長が150cmから160cmの間で，かつ体重が50kgから55kgまでの人数が全体の何%であるというように記入する。これを結合分布，または二次元分布という。同様にして三次元，四次元等々の分布も考えられるが，三次元以上は図示するのに困難であり，分布のようすを知るにはその特性量に頼らねばならない。

代表値

分布のようすを数量的に示す特性量の中でもっとも重要なものは平均値である。それはすべての測定値（一般的にいえば各個体に付随する標識としての数値）を加えて，その和を集団の数で割ったものである。このほかの代表値として中位数（メジアンともいう）がある。それは数値を大きさの順に並べたとき中央に位置する値をいう。いま標識の値がX₁，X₂，……，X_nであるとき，平均値は（X₁－m）²＋（X₂－m）²＋……＋（X_n－m）²を最小にするmの値として特徴づけられ，そのときのmをXとかく。同様にして，中位数は｜X₁－m｜＋｜X₂－m｜＋……＋｜X_n－m｜を最小にするmであり，これをmed Xと書くことが多い。

分散度

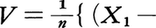
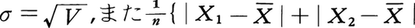
集団の標識の値X₁，X₂，……，X_nは代表値の両側に分布しているが，その散らばり方にはいろいろな可能性がある。代表値の近くに密集していることもあれば，両側に幅広く散らばっていることもある。この分散度を表すのに分散V，標準偏差σ，平均偏差などがある。それらはいずれもX_iとXとの差，すなわち偏差X_i－Xから求めら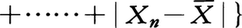れ，が平均偏差である。両者はそれぞれとも書くことができる。集団の標識を小さいものから順に並べて，四つの個数の等しいクラスに分けるとき，クラスの限界になる三つの数値を小さいほうから第1，第2，第3四分位数といい，それぞれQ₁，Q₂，Q₃と書く。Q₃－Q₁を四分位偏差と呼ぶが，簡単に求められ，それによりある程度分散度がわかるので，標準偏差の代りに用いられることがある。

　関連する特性値としては，平均値のまわりの高次のモーメントがある。p次モーメントμ_pは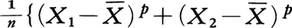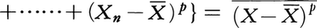と定義する。これらを用いて分布の非対称度（歪度）がμ₃²/μ₂³で，尖度がμ₄/μ₂²－3で定義され，いずれも分布の型をいうのに役だつ量である。

関連度

各個体に2種類の標識があって，それらの値をX₁，X₂，……，X_n，Y₁，Y₂，……，Y_nとしよう。Xのほうが大きくなるにつれてYのほうが大きくなる傾向があるか（正の相関がある場合），それとも逆の傾向があるか（負の相関がある場合），問題の2標識の関連の度合を表す量として共分散C_x,yや相関係数r_x,yがある。それらは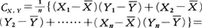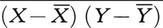および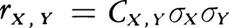で計算される。ここにσ_x，σ_yはそれぞれX，Yの標準偏差である。r_x,yは－1と1との間にあり，r_x,y＞0，またはr_x,y＜0に従って正または負の相関がある。－1または1に等しいときXとYは一次関係にある。r_x,y＝0のときは無相関であるといい，一方の分布状況は他方の値によって変わらない。このほか，3種類以上の標識があるとき，それらの相互関係は偏相関係数や重相関係数などを用いて数値的に示すことができる。

　これまでは標識として，ある量の測定値を例として説明してきたが，ほかにも男女の出生率のように，男児106対女児100という比率でほぼ一定していて集団的規則性をもつものについても，視点を変えてみれば，同様に記述統計学の対象とすることができる。

推測統計学

ピアソンの研究は記述統計学の完成に大きな貢献をしただけでなく，それから自然に母集団の概念が導入されるような新しい段階にまで到達することができた。母集団とは観測可能な個体からなる集団，あるいは人為的にそのようにみなされる対象であって，それから観測のため抽出された個体，あるいは試行の結果は母集団の特徴を伝える標本である。例えば風邪をひいた高熱の患者n人に，ある解熱剤を与えて平均1℃だけ熱が下がったとする。この現象は解熱剤の効果を論ずるうえでどれだけのことを意味するであろうか。もし効果があるとすれば，将来を通じすべての風邪ひきの患者に投与したい。いま試みられたn人はそのごく一部分の人にすぎない。このとき将来も含めた患者全体（理想的なものと考えた）が母集団であり，それに対して薬が効くかどうかという性質を知るために抜き出されたn人は標本である。この目的のために標本として選ばれる人数は多いほどよく母集団の性質を代表するであろう。実際問題としてはnを無限に大きくするわけにはいかない。ではどの程度にとれば目的は達せられるのか。また偏った標本のとり方をすれば当然母集団のよい代表とはならないが，その事情はどうであろうかなどを知るためには確率論的考察が必要となる。またn回の銅貨投げをみるとこれも標本と考えることができる。無限に多くの回数だけ銅貨を投げたと想定したら，それが母集団であり，もし銅貨がゆがんでいることがあるかもしれないとすれば，表の出た頻度をp，裏の出た頻度をq＝1－pとしなければならない。いま投げたn回はそのような母集団からの標本とみなされる。確率論のことばでいえば，確率空間は表の出る事象と裏の出る事象の二つだけを考えればよく，それぞれの確率をpおよびq（＝1－p）とする。標本はこの空間の上で定義され，値1（表）を確率pで，値－1（裏）を確率qでとるn個の独立な確率変数の系X₁，X₂，……，X_nである。解熱剤の例でも，i番目の患者が薬を服用してから下がった温度をX_iと表せばよい。わかっていることはX＝1ということである。

　ここで注意したいことは，平均値Xは記述統計学の場合と違って見本の平均値であるという理解から見本平均と呼ぶ。それは依然として確率変数であって，母集団からの選び方によって種々の値をとり，分布が対応している。銅貨投げの場合，nが大きいとき，大数の法則によりXはp－qに十分近い値をとる。

　標本平均以外にも標本の関数であって，母集団の特性を記述するものがたくさんあり，総称して統計量と呼ばれる。種々の統計量を選び，その確率分布をみて，母集団のパラメーターの推定を考えたり，統計的な仮説の検定を行うのが推測統計学（推計学ともいう）の目標である。まず基本となる母集団の分布が多くの場合正規分布，あるいは近似的に正規分布に近いとしてよいことに注意する。その分布は平均値mと分散σ²によって一意的に決まり，密度関数g（x;m，σ²）は次式で与えられる。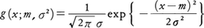実際，前述の解熱剤の例でいえば，その効果は下がった体温の量で表され，基本的にはある定まった値（平均値m）であるが，患者の体質や病状などに個人差があって，mからの偶然誤差が生ずる。この誤差の分布は，中心極限定理の教えるところによって正規分布と仮定するのが妥当であることがわかる。解熱剤の平均的効果を知るには，得られた標本からmの値を推定することになる。当然Xがmの推定値を与えていることが予想されるが，どの程度の信頼できる推定であるか，ほかによりよい推定値がないかなど確率論の知識に頼って判断しなければならない。同様なことが銅貨投げの場合についてもいえる。銅貨がゆがんでいるかどうかの判断は，標本によってpが1/2に等しいかどうかをみることになる。銅貨投げの確率分布はよく知られているように二項分布であるが，nが大きいときは正規化（平均値を0に，分散を1になるよう線形変換を施す）すれば近似的に標準正規分布に近いことがわかっている（中心極限定理）。よってpについての仮説p＝1/2を検定しようとすれば，近似的ではあるが，正規分布から導かれるいくつかの分布を用いることになる。そこで推定論や検定論を展開するための基礎として，母集団の分布が正規分布である場合（正規母集団）の各種統計量の分布を準備する。

正規母集団の場合の各種統計量の分布

母集団の分布が平均値m，分散σ²の正規分布の場合を考える。必要に応じて簡単のためm＝0，σ²＝1の標準正規分布をとることがある。また標本の大きさはnとする。（1）標本平均Xはやはり正規分布に従い，平均値は0で，標準偏差は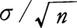である。解熱剤の場合，n＝100としたときXは平均値m，標準偏差σ/10の正規分布に従う。すなわちXはmに十分近く，そのXが1であったのでmは十分1に近いものとして推定できる。

（2）χ_n²＝X₁′²＋X₂′²＋……＋X_n′²，X_i′＝（X_i－m）/σ_iなら，χ_n²の分布は自由度nのχ²（カイ2乗）分布に従う。その分布の密度関数k_n（x）は，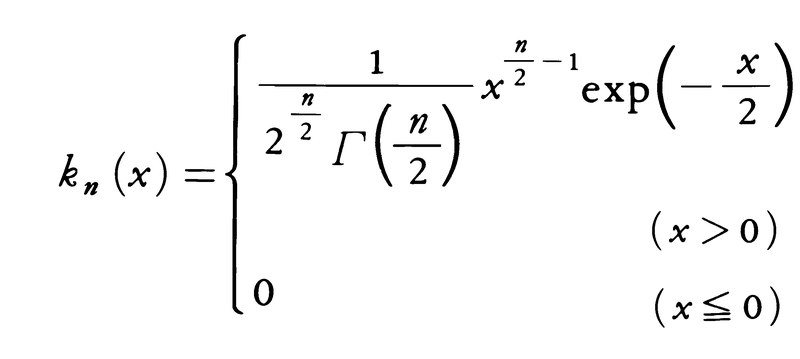

である。その平均値はn，分散が2nであることはすぐにわかる。関連する統計量として，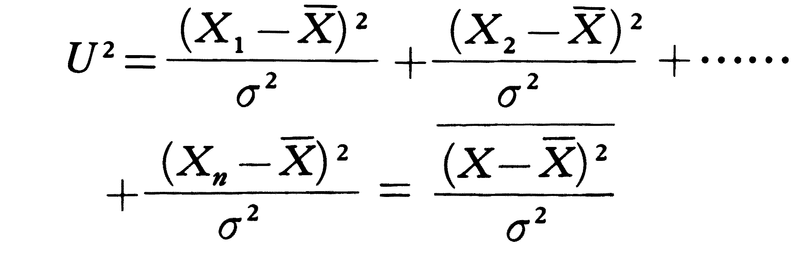

があるが，これもχ²分布に従う。しかし自由度はn－1である。

（3）X₀，X₁，X₂，……，X_nは平均値が0，分散σ²の正規分布に従う独立な確率変数（すなわちm＝0である正規母集団からの標本）とする。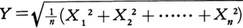とおき，統計量tを，

　t＝\(\frac{X0}{Y}\)

で定義する。このtの分布関数S_n（x）＝P（t≦x）は密度関数s_n（x）＝S_n′（x）をもち，それは，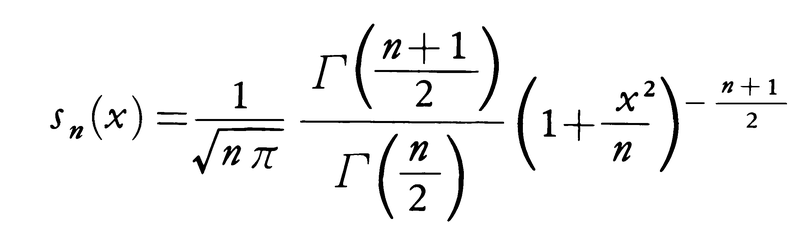

と表される。分布関数S_n（x），あるいは密度関数s_n（x）をスチューデント分布またはt分布といい，ゴセットWilliam Sealy Gosset（1876-1936。ペンネームがStudent）によって初めて統計の問題に用いられた。nはこの分布の自由度である。この分布は結果として母集団分布の分散σ²に無関係となる。それはtがXについて0次の斉次式であることから当然であるが，応用上この注意は重要である。t分布の特徴として，ほかにs_n（x）が原点Oに関して対称であること，（n－1）次までのモーメントが存在すること，nが大きくなるとs_n（x）は標準正規分布の密度関数に十分近くなることなどがあげられる。

（4）同じく平均値が0，分散がσ²の正規母集団から，大きさn＋mの標本X₁，X₂，……，X_m，Y₁，Y₂，……，Y_nが得られたとき，X²＝X₁²＋X₂²＋……＋X_m²，Y²＝Y₁²＋Y₂²＋……＋Y_n²

とおいて統計量，

　k＝\(\frac{X}{Y}\)

を考える。このときkの分布関数は密度関数f_mn（x）をもち，その関数形は，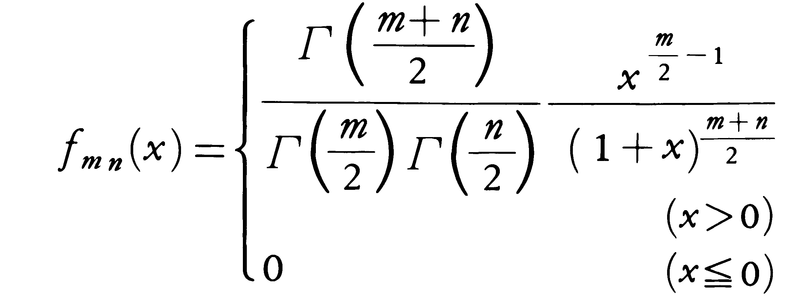

である。この分布も母集団の分布の分散σ²を含まない。R.A.フィッシャーは分散分析を展開するにあたり，kに関連して次式で定義される統計量zを導入した。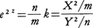zの分布の密度関数は上記のf_mn（x）を用いて次式で与えられる。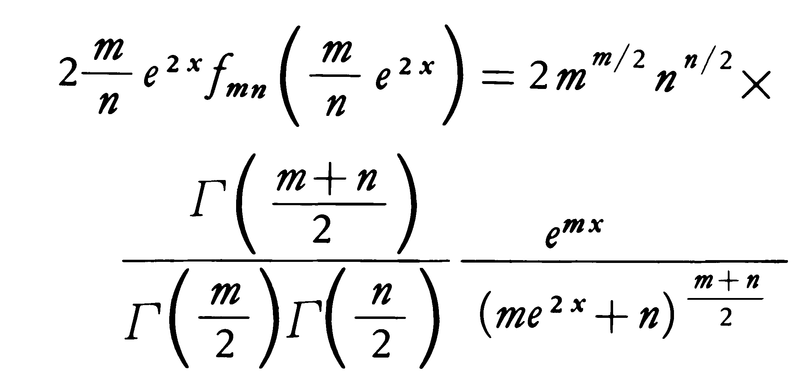

この分布はフィッシャーのz分布と呼ばれることがある。組（m，n）はその分布の自由度である。なお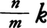，の分布は自由度対（m，n）のF分布と呼ばれる。

（5）上の（4）と同じ記号を用いて，統計量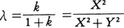，を定義する。明らかに0≦λ≦1であり，λの分布は［0，1］に集中する。この区間で密度関数が定義され，それは前出の記号f_mn（x）を用いて，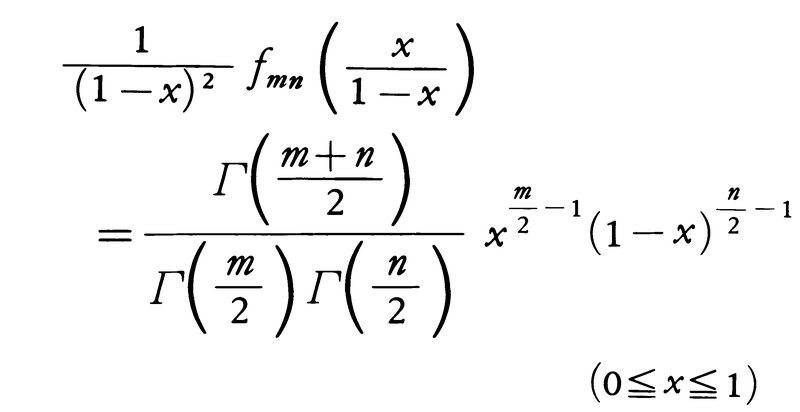

と表される。この分布はベータ分布と呼ばれ，やはり推測統計学でたいせつな役割を果たす。ちなみに上式右辺の係数はベータ関数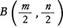の逆数に等しい。

（6）標本相関係数　母集団の分布が二次元正規分布で，相関係数がρの場合を考える。密度関数は，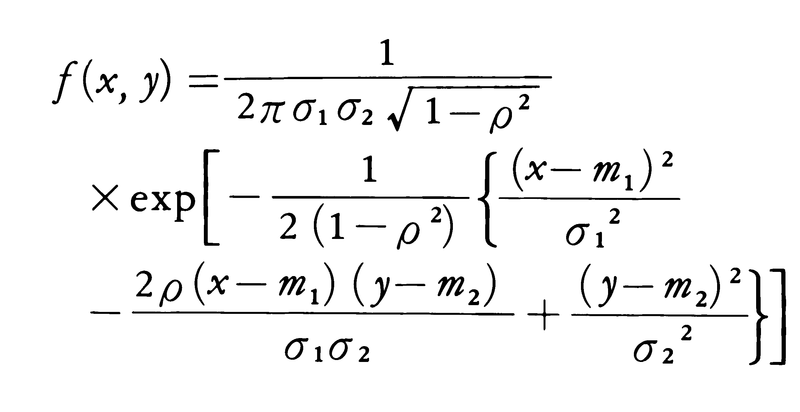

と表される。したがって標本は2種類の標識の実現値（X₁，Y₁），（X₂，Y₂），……，（X_n，Y_n）として記述される。このとき標本相関係数rは，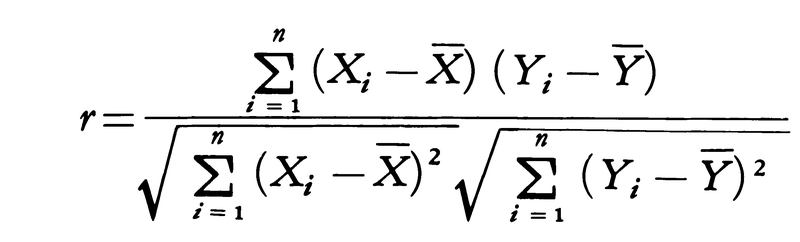

で表される統計量である。rの分布関数も密度関数p（r，ρ）をもち，

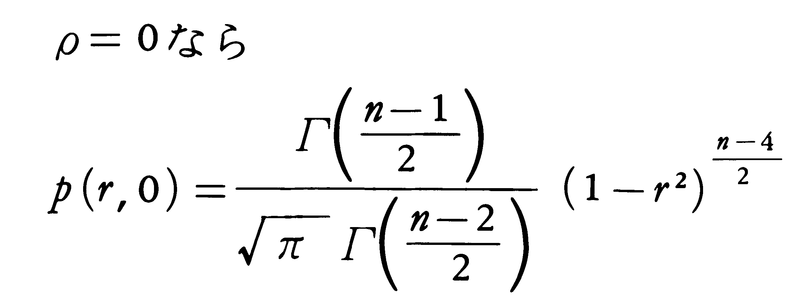
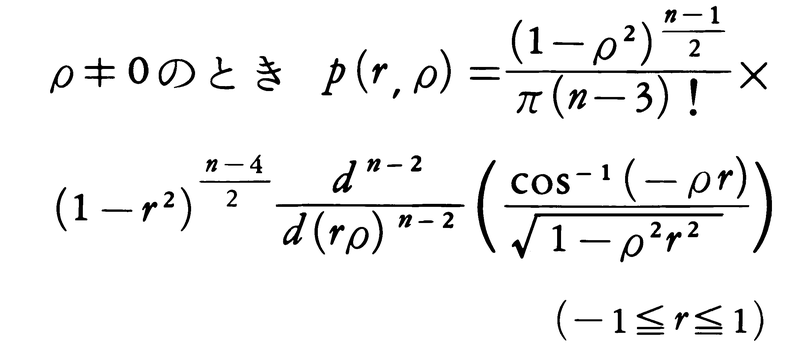
である。

　以上の諸統計量の分布を用いて，推測統計学の課題である推定や検定の問題を主として正規母集団の場合に論じよう。

推定

観測値Xが未知のパラメーターθを含む確率分布に従って変動しているとする。Xからなんらかの方法で，あるいはXの適当な関数を選んで，θの一つの推定量θ＾を作る。詳しくいえば，同じ上記の分布に従う独立な確率変数，すなわち標本X₁，X₂，……，X_nをとり，その関数としての推定量θ＾＝θ＾（X）をとる。このθ＾はなるべく真の値θに近いようにくふうされねばならない。よい推定値であるための条件として，第1に不偏性があげられる。それは，θ＾（X）は確率変数X₁，X₂，……，X_nの関数として，それ自身確率変数であるが，その平均値がθに一致すること，すなわち条件，

　E＝（θ＾（X））＝θ

を満たすものである。直観的にいえば，この関数θ＾を用いた推定を何度も標本をとって繰り返し行えば，平均的には真のθとだいたい同じとみなせるということで，不偏性はごく自然な要請といえよう。そのような不偏推定値の中で，θのまわりの分散（それは推定誤差の大きさとみなされる），V（θ＾（X））を最小にするものθ＾^*（X）があればより好ましい。このθ＾^*は（一様）最小分散不偏推定値と呼ばれる。ここで用いた分散はクラメール=ラオの不等式によってその下限が知られている。この限界に一致する分散をもつ不偏推定量を有効推定量という。

　例1　正規母集団があって，分布の平均値（母平均）と分散（母分散）がそれぞれm，σ²だとする。

（1）標本平均Xはmの不偏推定値であるばかりでなく，実は有効推定量になっている。（2）母平均mが知られているとき，標本分散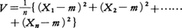，はσ²の不偏推定値で，かつ有効な推定値になっている。

（3）もし母平均mが知られていなくて，σ²を推定しようとするとき，mをXで代用し，不偏推定値，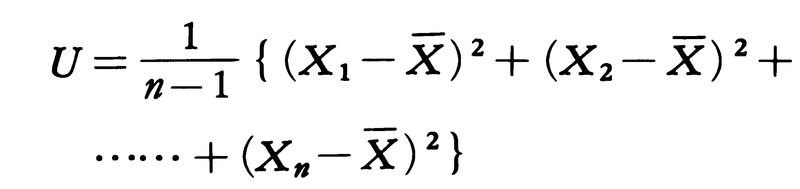

をとればよいが，これは有効推定値とはならない。

　次に望ましい推定量として充足（十分）推定量がある。母集団の分布の密度関数をf（x，θ）とかく。ここにθは推定したい未知のパラメーターである。標本は独立確率変数の列だから，（X₁，X₂，……，X_n）の分布の密度関数は積f（x₁，θ）・f（x₂，θ）・……・f（x_n，θ）で与えられる。もしこの積が推定量θ＾の密度関数h（θ＾，θ）を用いて，

　h（θ＾，θ）・g（x₁，x₂，……，x_n）

と書けるとき，θ＾をθの充足推定量という。上の積でgはθに無関係である。そのことはθに関する情報はh（θ＾，θ）のほうだけから提供される。すなわち，それはθ＾の中に含まれ，しかもそれで十分であるという意味でこの名が与えられた。

　例2　例1と同じく正規母集団をとる。標本分散Vは母分散σ²の充足推定量であるが，mが未知のときのσ²の不偏推定量Uは充足推定量ではない。

　これまでと少し違った観点から推定量を求める方法として最尤（さいゆう）法がある。母集団の分布がパラメーターθを含む密度関数f（x，θ）で表されるとする。観測値x₀が得られたとき，そのx₀を固定してf（x₀，θ）をθの関数とみて，それを最大にするようなθの値θ＾を真のθの推定値としようというのがアイデアで，θの関数とみたf（x₀，θ）を尤度関数，θ＾を最尤推定量という。いくつかの観測値が得られた場合も，同様な考え方で最尤推定値を求めることができる。

　例3　母集団の分布は平均値m，分散σ²の正規分布とする。大きさnの標本が得られた場合，それらは互いに独立だからベクトル（X₁，X₂，……，X_n）の同時分布は，前出の密度関数g（x;m，σ²）を用いて，積，

　L（m，σ²）＝g（x₁;m，σ²）・g（x₂;m，σ²）・

　　……・g（x_n;m，σ²）

を密度関数とするものである。各x_iを標本値X_iでおきかえたL（m，σ²）が尤度関数である。そのとき，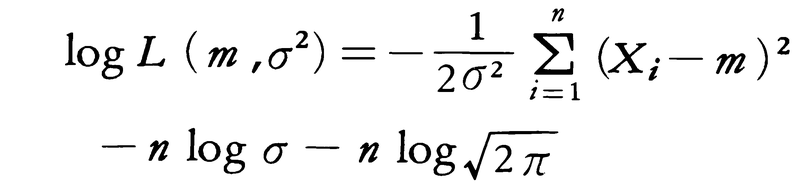

で，これを最大にするm，σ²の値はそれぞれ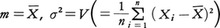である。したがって最尤推定値m＾＝X，σ＾²＝Vが得られた。m＾はすでに見たとおり不偏推定量，とくに有効推定量であるが，VのほうはE（V）＝（n－1）σ²で不偏推定値にはなっていない。

　これまでは，未知パラメーターθを推定するのに，候補となる1点を指示する点推定であったが，これとは異なり，パラメーターの存在しうる範囲を得られた標本から推定する区間推定の方法がある。標本X₁，X₂，……，X_nが得られたとき，θの動く範囲S（X）＝S（X₁，X₂，……，X_n）を適当に選んで，P（θ∈S（X））≧1－αとできるとき，S（X）を信頼係数1－αの信頼域という。S（X）を区間にとることが多く，そのとき信頼区間といい，この方法は区間推定と呼ばれる。

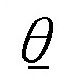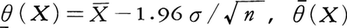
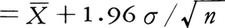　例4　分散σ²が知られている正規母集団では，信頼係数0.95の信頼区間を標本平均Xを用いてS（X）＝［ （X），θ（X）］，ただし

として与えることができる。

　再び最尤法の手法に返ってみよう。この方法はフィッシャーによる統計学上のもっとも大きな貢献であったといえる。しかし，彼の理論では分布の関数形はわかっていて，パラメーターのみが未知とする立場をとっている。ところが尤度関数の意味を問いなおせば，情報量，あるいはエントロピーの概念が重要な役割を果たしていることに思いあたる。これから1973年に赤池弘次（1927-　）によって提唱された情報量基準AICの概念を理解する手がかりが得られよう。それは次式で与えられる。

　AIC＝（－2）log_e（最大尤度）＋2（パラメーターの個数）

これを最小にするようなモデルを構成することにより，分布の型を推定することができるようになった。定常時系列のスペクトルの推定をはじめ，応用範囲も広く，数理統計学に新しい思想と手段を与えたものとして画期的な貢献といえよう。

検定

統計的な仮説の検定法は多様性をもっていて，考え方のうえでも議論されなければならないところも多い。以下ではよく用いられるものを例によって示すことにする。

　前述の銅貨投げの例で，例えば20回投げて表が16回も出たとしよう。ゆがんでいない銅貨なら表が出るのは10回前後であろうと推察される。もちろん投げた結果は偶然に支配されるので，全回裏が出ることも少ない可能性ながらありうることで無視できないが，表が出るのは10回前後の回数になることが自然だと思われる。16との差6は何を意味するであろうか。この意味を考えるには次のようにするとよい。もし銅貨がゆがんでいないとすれば，表の出る確率は1/2である。20回の銅貨投げの結果は二項分布で記述され，20回とも表が出る確率は0.000001程度，1回だけ裏が出るのは0.000019程度，……と数表あるいは計算機で調べることができて，16回あるいはそれ以上表の出る確率はほぼ0.006で1%にも満たない。これはめったに起こらないことが現実に起こったのであり，ゆがんでいないとした仮説は捨てることが望ましい。そうしても言い損なう危険は1%以下である。このような場合，仮説を棄却するといい，棄却される仮説を帰無仮説という。この例では1%を目安としたが，5%の水準のほうがむしろよく用いられ，これらの確率は有意水準と呼ばれている。仮説が棄却される場合に，仮説は有意水準1%（または5%）で有意であるという。

　このような仮説の検定法は，実際面では正規母集団について，平均値や分散に関する推論に用いられることが多い。以下の例は再び正規母集団についてである。

　例1　母分散σ²が知られていて，平均値mがm₀とは異なることを検定する場合，m＝m₀という仮説のもとでは，標本平均Xから計算される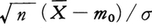量が標準正規分布に従うことを用いて，\(\sqrt{n}\)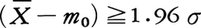ならば有意水準5%で有意であるとして検定（両側検定）される。事情により片側検定なら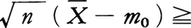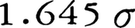を用いてもよい。

　例2　上の例で，σも未知としたときの仮説m＝m₀の検定には次のような方法がある。mおよびσの充足推定量として，それぞれ標本平均X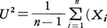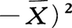とをとる。ここでσの値のいかんにかかわらず，つねに正しい結論を得るようにするには，m＝m₀のときσの値と無関係な分布をもつ統計量を用いる必要がある。XとUとが独立になることが知られるので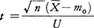をとれば，それが自由度n－1のt分布に従うことがわかり，t分布の表からα%点t_αを求めて，

　両側検定なら｜t｜＞t_α/2で，

　片側検定ならt＞t_αで

有意水準α%の検定を行うことができる。

　同様な考え方で，χ²分布を用いてσ²＝σ₀²の検定もできる。また二つの分散の相等性の検定はF分布を用いて行われる。相関係数に対するρ＝0の検定は，標本から得られる相関係数，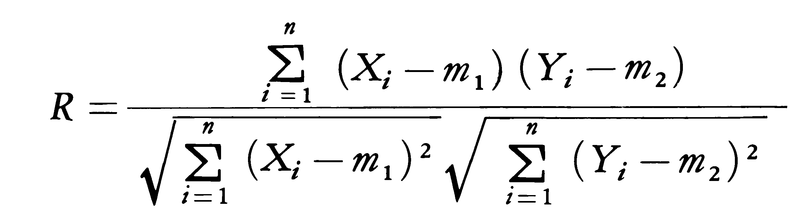

を用いて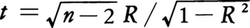，が自由度n－2のt分布に従うことを利用して，同様な考えで行うことができる。

標本抽出法

これまで述べてきた推定論，検定論は，いずれも母集団の分布をその分布とする独立確率変数列とみなしうる標本がえられたとして議論を進めてきた。これらの理論を実際問題に応用しようとするとき，そのような理想的な標本が得られるようなくふうが必要である。母集団からの抽出にはいわゆる無作為抽出であることが望ましい。また標本の大きさnも，大きいほどより正確な推論ができることは当然であるが，標本平均の分散がnに反比例して小さくなる事実も参考にしたいことである。また，母集団がいくつかの層に分かれているとき，適当なウェイト（重み）で標本の層別抽出を行うことは正確さを増すうえで重要である。

時系列の解析

時間とともに変化する偶然現象を時系列，または確率過程という。例えば気温は季節的な変動のほかに偶然に支配されて刻々と変動している。銅貨投げで，表の出た回数の累加も，試行回数を時刻とみれば時系列の例となる。いくつかの時点を選んでそこでの同時分布が定義されるが，この分布が時間の推移に関して不変であるとき定常時系列という。それについて，時刻tにおける値とt＋hでの値との共分散（それはhのみの関数），γ（h）は，この時系列についての重要な特性量である。あるいは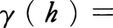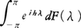とスペクトル分解したときのスペクトル測度dF（λ）を特性量とみてもよい。この推定には種々の統計的手法が用いられ，実際面への応用からいっても重要な数理統計学の分野となっている。

その他

数理統計学の課題としては，このほかにも線形モデルの構成，分散分析，多変量解析，情報理論など，歴史的にも，また実用的にも重要な項目がたくさんあり，数学的な研究手法も豊富になってきている。統計学の起源からいって生物学との関連も深く，力学の諸問題にもその解決の手段を与えるなど，数理統計学はもっとも重要な応用数学の分野である。
→統計学
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

数理統計学
すうりとうけいがく

「統計学」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の数理統計学の言及

【統計学】より

…
［理論統計学］
　理論統計学は，官庁統計のみならず，一般に集団的現象に関する数字データを扱う方法を考察する。それは一般に数理統計学とも呼ばれるが，数学的論理にのみ尽きるものではなく，一般に数字データの本質，その意義などを方法論的に吟味することも必要である。理論統計学の主要な分野は統計的データの分析法，および統計データの作成法の二つからなる。…

【ピアソン】より

…ケンブリッジ大学で数学を学び，ロンドン大学の教授となる。F.ゴールトンの影響により，生物学における統計的方法に興味をもつに至り，ゴールトンとともに雑誌《計量生物学Biometrika》を創刊し(1901)，また近代的数理統計学の基礎を築いた。その主要な貢献としては，相関係数の定義，回帰分析の方法の確立，χ²適合度検定法の発明，〈ピアソン系分布〉の導入，統計量の大標本のもとでの〈蓋然（がいぜん）誤差〉の計算，母数推定の積率法の提案などがある。…

※「数理統計学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」