二項分布（読み）ニコウブンプ

デジタル大辞泉

にこう‐ぶんぷ〔ニカウ‐〕【二項分布】

ある試行において、事象Eが起こる確率をp、起こらない確率をqとし、独立にn回試行するとき、その事象Eがr回起こる確率_nC_rp^rq^n－rの分布の状態。

出典　小学館

精選版 日本国語大辞典

にこう‐ぶんぷニカウ‥【二項分布】

1. 〘 名詞 〙 確率分布の一つ。ある試行で、確率事象Ｅの起こる確率がｐであるとする。この試行をｎ回独立に行なうとき、Ｅの起こる回数をｘとするとｘは０、１、２、…、ｎというｎ通りの値をとる確率変数で、x=k となる確率は _nC_kp^kq^n-k （k=0,1,2,…,n かつ、q=1-p）となる。この確率変数ｘの分布をいう。_nC_kp^kq^n-k が二項式 p+q のｎ乗を展開したときの一般項であるところからこの名がある。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

二項分布
にこうぶんぷ

ある試行において事象Eのおこる確率をpとする。この試行を独立にn回繰り返す場合にEのおこる回数をXと置くと、Xは確率変数であって、X=kとなる確率p_k=P(X=k)は、q=1-pとして次式で与えられる。

　　p_k=_nC_kp^kq^n-k
　　　　　(k=0,1,……,n)
この確率分布を二項分布といい、B(n,p)と表す。

〔例1〕さいころを4回投げて、そのうちちょうど2回6の目の出る確率は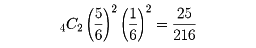

である。

　前記のnC_kp^kq^n-kは、(q+p)ⁿを二項定理によって展開した式
　　_nC₀qⁿ+_nC₁pq^n-1+……
　　　+_nC_kp^kq^n-k+……+_nC_npⁿ
の項になっている。二項分布B(n,p)において、kを横軸に、p_kを縦軸にとって(k=0,1,2,……,n)、折れ線グラフをつくると次のようになる。k₀=np+p-1が整数であれば、p_kはk＜k₀で単調増加、k=k₀,k₀+1で最大値をとり、k＞k₀+1で単調減少である。np+p-1が整数でなければ、np+p-1の整数部分をk₀とするとp_kはk＜k₀で単調増加で、k=k₀で最大値をとり、k＞k₀で単調減少である。初めに述べた二項分布の定義から次のことが導かれる。確率変数X₁、……、X_nは独立で
　　P(X_i=1)=p, P(X_i=0)=q=1-p
　　(i=1,……,n)
とする。このとき確率変数
　　X₁+X₂+……+X_n
の確率分布は二項分布B(n,p)である。二項分布B(n,p)の平均値はnp、分散はnpqであり、特性関数は(pe^it+q)ⁿである。

〔例2〕さいころを500回投げるとき、1の目が80回以上出る確率pを求めよ。

　求める確率pは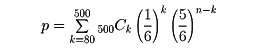

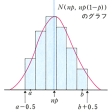
であるが、この値を直接計算することは容易でない。このような形の問題に対しては、次のように正規分布表を用いて計算を行う。二項分布の正規分布による近似確率変数Xの分布が二項分布B(n,p)であるとき、nが大きければ、確率変数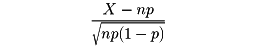

の分布は標準正規分布に近い（ラプラスの定理）。このことを利用して前の〔例2〕の確率pの近似値を求めることができる。0≦a＜b≦nである二つの整数a、bに対して、p(a≦X≦b)は図の青色部分の面積で、これはXと同じ平均および分散をもつ正規分布N(np,np(1-p))のグラフとx軸および2直線
　　x=a-0.5, x=b+0.5
で囲まれた部分の面積とほぼ等しい。したがって、Zの分布を標準正規分布として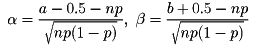

と置けば、次の近似式が成り立つ。

　　P(a≦X≦b)≒P(α≦Z≦β)
この式により正規分布表を用いて〔例2〕のpを求めるとp=0.67が得られる。

［古屋　茂］

二項分布の例〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

二項分布 (にこうぶんぷ)
binomial distribution

毎回独立に同じ偶然に支配される試行を繰り返す場合，各試行で二つの可能性（かりにそれらを成功および失敗と呼ぶ）しかないとき，これをベルヌーイ試行という。成功および失敗の確率が，それぞれpとq＝1－pであるn回のベルヌーイ試行において，ちょうどk回成功する確率をb（k;n，p）とかけば，

　b（k;n，p）＝_nC_kp^kqⁿ⁻^k

　　　　　　　　　（k＝0，1，……，n）

である。これを二項分布という。この分布の平均値はnpで分散はnpqである。確率b（k;n，p）はkが0から増加していくとき，k＜（n＋1）pの範囲では増加し，k＞（n＋1）pのときはkとともに減少する。もし（n＋1）p＝k₀となる整数k₀があるときはb（k₀;n，p）＝b（k₀－1;n，p）となる。

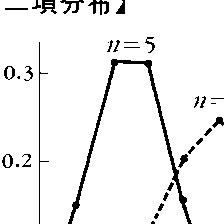
　この分布を平均値0，分散1となるように規格化して，すなわち，直線上の点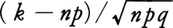（ただしk＝0，1，……，n）に確率b（k;n，p）を置いて得られる分布は，nが十分大きいとき，図のように標準ガウス分布に近いことが知られている（ド・モアブル=ラプラスの定理）。一方，nが大きくてもpが十分小さく，npがふつうの大きさであるときには，np＝λとおいて，ポアソン分布p（k，λ）（ただしk≧0）でよく近似される。
執筆者：飛田 武幸

図－二項分布

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

二項分布
にこうぶんぷ
binomial distribution

応用上しばしば用いられる確率分布の一つ。たとえば○×式で答える問題があるとし，この問題にまったくでたらめに答えて，10問中 8問が正答になる確率を求めるには，独立試行の回数 n＝10，10問中正答になる回数 r＝8，でたらめに○×をつけるから○をつける確率 p＝1/2，また q＝1－p＝1/2とおいて，次の公式を適用すればよい。いまその確率を Pr（X＝r）とおくと，

Pr（X＝r）＝_nC_rp^r（1－p）^n-r

すなわち，上の問題の答は

Pr（X＝8）＝₁₀C₈（1/2）⁸（1/2）^10-8＝0.044

となる。
ここに 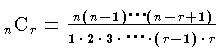で，二項係数である。一般にある事象 E の起こる確率を p とするとき，n 回の独立試行を繰り返すときに事象 E が現れる回数を指示する確率変数を X，実際に起こる回数を一般に r（r＝0，1，…，n）で示すと，X が値（実現値）r をとる確率 Pr（X＝r）が _nC_rp^r（1－p）^n-r で与えられ，二項分布といわれる。X は n＋1の値でしか正の値の確率をもたないから離散的である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

二項分布【にこうぶんぷ】

x＝０，１，２，…，nのそれぞれの値が出現する確率が　(/n)C(/x)p(x/)（１−p）(n/)(-/)(x/)で与えられる分布（０＜p＜１）。(/n)C(/x)はn個のものからx個を選ぶ組合せの数，つまり二項係数。平均値はnp，標準偏差は（式１）。たとえば不良率pの母集団からとったn個のサンプル中の不良品の個数xはこの分布に従う。→二項定理

出典　株式会社平凡社

法則の辞典

二項分布【binomial distribution】

離散分布の一つ．その確率関数は

f（x）＝nC_xp^x（1－p）^x

となる．

出典　朝倉書店

栄養・生化学辞典

二項分布

　ある事象Aが起こる確率がPである場合，試行をn回繰り返したとき，Aがx回起こるとしたときのxの分布．

出典　朝倉書店

世界大百科事典（旧版）内の二項分布の言及

【確率】より

…そのとる値は0,1,2，……，nで分布｛p_k；0≦k≦n｝はp_k＝_nC_kp^kq^n－kである。これを二項分布という。これは重要な離散形分布の例で，応用上もよく現れる。…

【確率分布】より

…　重要なのはF₁とF₂で，F₁は連続型，F₂は離散型であるという。
［離散型分布］
　(1)もっとも重要なものは二項分布であり，F(x)はx＝0,1，……，nのみで増加し，x＝kでの跳びは_nC_kp^kq^n－k(q＝1－p)である。これは成功する確率がpであるn回のベルヌーイ試行における成功する回数の分布である。…

※「二項分布」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」