微分トポロジー(びぶんとぽろじー)とは？意味や使い方

日本大百科全書(ニッポニカ) 「微分トポロジー」の意味・わかりやすい解説

微分トポロジー
びぶんとぽろじー

微分（可能）多様体の微分同相写像で不変な性質を研究する幾何学が微分トポロジーである。ユークリッド空間Rⁿの上半空間
　　｛x=(x₁,……,x_n)∈Rⁿ∈x_n≧0｝
をHⁿで示す。位相空間Mがn次元位相多様体であるとは、(1)Mが有限個の連結成分をもつパラコンパクトなハウスドルフ空間である。(2)Mの開被覆｛U_α｝_α∈Aと各αに対してHⁿの開集合V_αおよび同相写像h_α:U_α→V_αが存在する。Σ=｛h_α:U_α→V_α｝をMの局所座標系という。いま図Aのように
　　h_α:U_α→V_α,　h_β:U_β→V_β
がΣに属しU_α∩U_β≠∅とすれば、同相写像
　　g_βα
　　　=h_β゜h_α^-1:h_α(U_α∩U_β)
　　　→h_β(U_α∩U_β)
が得られる。g_βαをh_αよりh_βへの座標変換という。このg_βαが無限回微分可能であるとき、Mはn次元微分（可能）多様体という。もしg_βαがPL（部分的に線形）であるとき、MはPL多様体（または組合せ多様体）という。さらにRⁿのかわりにn次元複素ユークリッド空間をとるときg_βαは複素解析的であれば、このときMは複素多様体とよばれる。この微分多様体およびそれらの間の微分可能な写像のトポロジー的な性質を追究するのが微分トポロジーであり、三次元以下の場合には組合せトポロジー、PLトポロジーと同じことになる。次に微分トポロジーの基礎概念の二、三を紹介する。

［野口　廣］

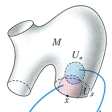
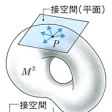
接空間

微分多様体Mがユークリッド空間の中にある場合、Mの各点で図Bのようにその点におけるMの接線の集合を考えると、Mと同じ次元のベクトル空間となる。このベクトル空間がその点におけるMの接空間である。Mの各点でこうした接空間を考え、その全体をT(M)で示し、Mの接ベクトル・バンドルという。同様に法線のMの各点での法ベクトル・バンドルなどを考える。一般にMの各点にベクトル空間を対応させたベクトル・バンドルが考えられる。この概念を一般化したものがファイバー・バンドルである。

［野口　廣］

臨界値とサードの定理

いまMよりNへの微分可能な写像f:M→Nが与えられたとする。するとその微分写像df:T(M)→T(N)が定まる。dfはMの接バンドルT(M)をNの接バンドルT(N)へと写す。すなわちdfはMの点Pにおける接線をf(P)におけるNの接線へと写す。ここでもし、fでMの点PがNの点Qに写り、Pにおける接空間がQにおける接空間の上へ写るとき、点Pはfの正則点であるといい、そうでないとき、すなわち、Mの接空間がNの接空間ではなくその部分空間へ写されるとき、点Pはfの特異点という。またNの点QはQへ写るMの点がすべて正則点であるときfの正則値であるといい、そうでないとき臨界値という。「f:M→Nの臨界値の集合はNの（ルベーグ）測度0の部分集合である」。これをサードの定理という。

［野口　廣］

モース理論

モース理論は1920年代にアメリカのモースHarold Marston Morse（1892―1977）が開拓した関数の特異点に関する基本的理論であり、次のモースの補題がその中心となっている。点Oが微分可能関数f:Rⁿ→Rの特異点であるとする。点Oにおけるヘッシアン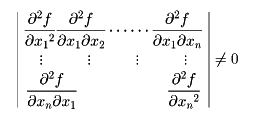

であるとき（すなわちOが非退化特異点である）、Oの周りの適当な座標変換
　　x=(x₁,x₂,……,x_n)
　　　→y=(y₁,y₂,……,y_n)
を行うと、関数fは
　　f(y₁,……,y_n)
　　　=f(O)+(1/2)(y₁²+y₂²+
　　　　……+y_r²-y_r+1²-……-y_n²)
となる。たとえばf(x,y,z)=x²+xy+y²+yz+z²+zxは原点で特異点であるが、ヘッシアンは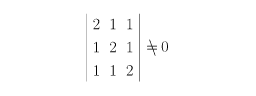

であるので、モースの補題により、
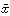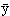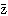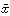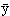　　f(,,)=²+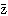²+²
へと変換される。