特異点（読み）トクイテン（その他表記）singular point
singularity

デジタル大辞泉

とくい‐てん【特異点】

１ 曲線・曲面上で、接線や接平面が存在しないか二つ以上ある点。
２ 重力の固有の大きさが無限大になってしまう点。ブラックホールは宇宙の特異点である。時空の特異点。
３ ⇒技術的特異点

出典　小学館

改訂新版　世界大百科事典

特異点 (とくいてん)
singular point
singularity

数学ではきわめて広い意味に使われる概念で，曲線，曲面，多様体，関数，微分方程式などが，一般のところに比べて異常な形態を示すところを意味する。関数論においては，関数fが0＜｜z－a｜＜rでは1価正則だが｜z－a｜＜rでは正則でないとき，aをfの孤立特異点という。このとき，0＜｜z－a｜＜rで，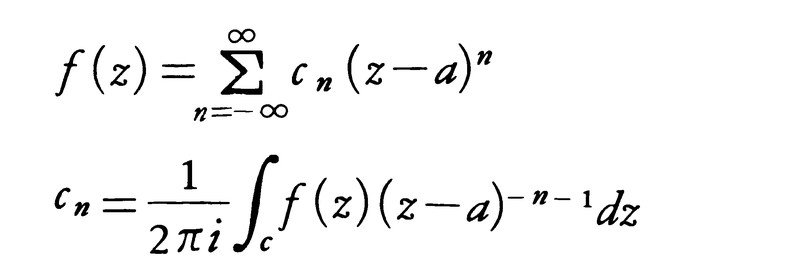

　（cは円周｜z－a｜r′，（0＜r′＜r）を正の向きにまわるもの）

が成り立つ。これをローラン展開という。また，添字が負のもののみの部分，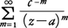

のことを，ローラン展開の主要部という。主要部が有限項を除いて係数が0のとき，aはfの極という。このときは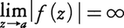，が成り立ち，また1/f（z）はaで正則となり，fの異常性は少ないので，特異点と考えない場合もある。例えば，有理関数においては，分母が0になる点はすべて極である。領域Dで定義されて，各点で正則であるか極であるような関数は，Dで有理型であるというが，このような関数は，極では値が∞であると考えて，正則関数とある程度同じように扱うことができる。次に，主要部の係数で0でないものが無限個存在するときは，aをfの真性特異点という。このときは，zのaへの近づき方によって，f（z）は任意の値に近づきうる（ワイヤーシュトラスの定理）。また，fはaの近傍で，たかだか一つの値を除いて，すべての値を無限回とる（ピカールの定理）。例えばf（z）＝e^1/zは0に真性特異点をもっている。

　やや一般的に，関数fが0＜｜z－a｜＜rで正則である（ということのみがわかっている）とき，aをfの孤立特異点と呼ぶ場合もある。そして，なんらかの方法でfが｜z－a｜＜rの正則関数に解析接続されるとき，aを除去可能な特異点という。例えばローラン展開の主要部の係数がすべて0なら除去可能である。また，fが0＜｜z－a｜＜rで有界なら，aは除去可能な特異点である。
執筆者：及川 広太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

特異点
とくいてん
singular point

(1) 曲線について　平面曲線 f(x，y)＝0 の上で，f_x(a，b)＝f_y(a，b)＝0 となるような点 (a，b) をこの曲線の特異点という。曲線が自分自身と交わっている点 (結節点) ，曲線から孤立はしているが，その座標が曲線の方程式を満たしている点 (孤立点) ，曲線の方向が逆になる点 (尖点。2つの分枝が1本の接線を共有する) などは曲線上の特異点である。しかし特異点という一般的な言葉のなかには，一般性が失われて，特異性が現れる点という意味があるので，以上の3つ以外にも，平面上で特異点と呼ばれているものがある。たとえば，曲線が自分自身に接する点 (自己接触点) ，曲線が急に方向を変える点 (角点。尖点とは異なって，その点に 2 本の接線が引ける) ，曲線がとぎれる点 (終止点) ，曲線が回りながら限りなくそこへ近づくような点 (漸近点) などである。特異点は，そのほか，曲面上の点についても定義される。 (2) 関数について　関数の正則性が破れる点をいう。特に複素関数について，解析的にならない点，つまりその点のまわりでべき級数展開ができない点である。 f(z)＝1/z では z＝0 が極，f(z)＝√z では z＝0 は分岐点，f(z)＝ log z では z＝0 は真性特異点といわれる特異点である。 (3) 微分方程式について　解の一意性が成立しなくなったり，その他の異常が生じる点を特異点という。微分方程式によっては，全体としては異常はないが個々の解が無限大に発散するなどの特異性を示す動く特異点をもつものもある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の特異点の言及

【代数曲線】より

…f(x,y)の次数がnのときn次曲線という。f(x,y)＝0で定義される平面代数曲線c上の点(a,b)は，のとき特異点と呼ばれる。のときは正則点と呼ばれる。…

【力学系】より

…Xの各点xに対し，｛φ_t(x)｜－∞＜t＜∞｝をxを通る軌道という。とくに1点となる軌道を特異点または平衡点といい，閉曲線となる軌道を周期軌道という。力学系の理論では，特異点や周期軌道の存在，t→＋∞またはt→－∞のときの軌道の挙動，軌道の大域的状態の小さな摂動による変化などがトポロジーの立場から研究される。…

※「特異点」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」