座標変換（読み）ザヒョウヘンカン（英語表記）coordinate transformation

デジタル大辞泉

ざひょう‐へんかん〔ザヘウヘンクワン〕【座標変換】

一つの座標系で表された座標軸を、平行移動・回転移動して別の座標系に表し変えること。

出典　小学館

精選版 日本国語大辞典

ざひょう‐へんかん ザヘウヘンクヮン【座標変換】

〘名〙 一つの座標系による点の座標や図形の方程式などを、別の座標系によるそれに表わし変えること。物理学では、同一質点に対する二つの座標系が相対的に運動している場合に用いる。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

座標変換 (ざひょうへんかん)
coordinate transformation

直線，平面や空間の点は一つの座標系を定めることにより，座標と呼ばれる数，または数の組によって表されるが，座標系が異なれば同じ点の座標も一般には異なる。しかしながら，二つの座標系が与えられたとき，これらの座標系に関する同一点の座標の間には一定の関係式が成り立つ。この関係式を座標変換式といい，これによって一つの座標系に関する座標を他の座標系に関する座標におきかえることを座標変換するという。

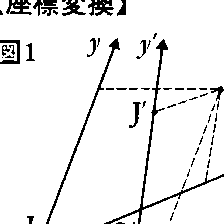
　例1　平面上にOを原点としI，Jを単位点とする平行座標系と，O′を原点としI′，J′を単位点とする平行座標系が与えられたとき，前者に関するO′，I′，J′の座標をそれぞれ（h，k），（a＋h，c＋k），（b＋h，d＋k）とすれば（図1），点Pのこれらの座標系に関する座標（x，y），（x′，y′）の間に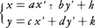，という座標変換式が成り立つ。とくに，OIとO′I′，OJとO′J′がそれぞれ平行で等しいときは座標変換式は，

　x＝x′＋h，y＝y′＋k

となる。これを座標系の平行移動という。また，両座標系が同じ点Oを原点とする直交座標系で，I，JをOのまわりにθだけ回転した位置にI′，J′があるときは（図2），座標変換式は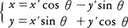，となる。これを座標系の回転という。

　例2　平面上の直交座標系に対し，その原点Oを極としx軸の正の向きを首線とする極座標系を考えれば（図3），点Pの直交座標（x，y）と極座標（r，θ）の間に，x＝rcosθ，y＝rsinθ，または逆に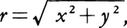，θ＝tan⁻¹（y/x）という座標変換式が成り立つ。同様に，空間の直交座標（x，y，z）と極座標（r，θ，φ）の間に，x＝rsinφcosθ，y＝rsinφsinθ，z＝rcosφ，または逆に，r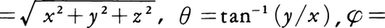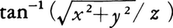という座標変換式が成り立つ。なお，力学系の座標変換については〈座標〉の項を参照。
執筆者：中岡 稔

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

座標変換
ざひょうへんかん
transformation of coordinate system

ある座標系で記述された数学的対象 (たとえば点) や物理現象を，別の座標系でみたらどうなるかという問題は，学問的にしばしば基本的な重要性をもつ。たとえば平面上の点 P の座標が，一つの座標系では (x，y) で，別の座標系では (x'，y') で表わされているとき，x および y を，x' および y' の関数と考えれば，x ，y はそれぞれ x＝f(x'，y') ，y＝g(x'，y') と書ける。これは座標 (x，y) で記述された点 P を，別の座標 (x'，y') で記述しなおすわけで，このようなことを一般に座標変換といい，上述の関係式を座標変換の式という。これはまた，同一の対象が2種類の座標系で記述されているとき，それら2つの座標系によって定まる座標の間の関係を定めることと言い換えてもよい。また，特にユークリッド空間内で，原点を共有する2つの直交座標系の間の座標変換を直交変換という。たとえば直交座標系 O－xy ，O－x'y' において，x 軸および x' 軸が正の方向に関して θ 度で交わっているとき，同一の点 P の2つの座標 (x，y) および (x'，y') は x＝x' cos θ－y' sin θ ，y＝x' sin θ＋y' cos θ という直交変換の式で関係づけられる。ここで原点 O からの距離は，直交変換によって不変である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

座標変換【ざひょうへんかん】

空間で二つの座標系を考えたとき，同一点のそれぞれに対する座標（x，y，z）と（x′，y′，z′）との間に成り立つ関係式　x＝f（x′，y′，z′），y＝g（x′，y′，z′），z＝h（x′，y′，z′）を座標変換という。直交座標における座標変換は座標軸の平行移動と回転。→座標
→関連項目ローレンツ変換

出典　株式会社平凡社

世界大百科事典（旧版）内の座標変換の言及

【座標】より

…ニュートンの運動方程式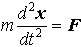，は，ある時刻におけるx，およびdx/dtの初期値が与えられた場合，これに対して一つの軌道が定まることを示している(mは物体の質量，Fは力)。
［時間によらぬ座標変換］
　運動する質点を表すのに，座標系は一つときまっているわけではなく，観測者にとってつごうよく変えることができる。一つの座標系を他の座標系に変えるやり方は，一般に同一の点Pの二つの座標x(x,y,z)とx′(x′，y′，z′)との間の関係式を与えることによって定まる。…

【相対性理論】より

…これがアインシュタインをして現代でももっとも魅力ある物理学者の一人たらしめている原因であろう。ここではまず座標変換，慣性系など，相対性理論の理解のための予備知識の説明から始め，次いで特殊相対性理論，一般相対性理論について概説したい。アインシュタイン
【運動の相対性と座標変換】
　およそ運動とは，すべて，〈何か〉に対する運動として記述される。…

※「座標変換」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」