方向余弦（読み）ほうこうよげん（英語表記）direction cosine

精選版 日本国語大辞典

ほうこう‐よげん ハウカウ‥【方向余弦】

〘名〙 解析幾何学で、空間の有向直線が各座標軸となす角の余弦（コサイン）のこと。

出典　精選版 日本国語大辞典

デジタル大辞泉

ほうこう‐よげん〔ハウカウ‐〕【方向余弦】

解析幾何学で、直線の方向を示す数。直線が三次元の直交座標において各座標軸となす角の余弦（コサイン）のこと。

出典　小学館

改訂新版　世界大百科事典

方向余弦 (ほうこうよげん)
direction cosine

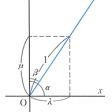
直交座標系の与えられた空間に向きのついている直線gがあるとき，原点Oからgの向きに引いた長さ1の半直線OPがx軸，y軸，z軸の正の向きとなす角をそれぞれα，β，γとすれば，Pの座標（l，m，n）はl＝cosα，m＝cosβ，n＝cosγで与えられ，l²＋m²＋n²＝1が成り立つ。（l，m，n）はgの方向を与え，上のように余弦で表されるので，gの方向余弦と呼ばれる（図）。向きのついた直線g′がもう一つあって，その方向余弦が（l′，m′，n′）ならば，gとg′のなす角をθとすれば，cosθ＝ll′＋mm′＋nn′が成り立つ。向きのついていない直線については，その直線に任意の向きをつけたときの方向余弦をもって，その直線の方向余弦と定義する。したがって（l，m，n）を方向余弦とする直線はまた（－l，－m，－n）も方向余弦とする。点（a，b，c）を通り（l，m，n）を方向余弦とする直線の方程式は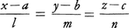，である。
執筆者：中岡 稔

図－方向余弦

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

方向余弦
ほうこうよげん

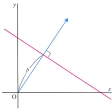
与えられた方向の単位ベクトルの正規直交基底に関する成分を、その方向の方向余弦という。すなわち、平面上にゼロでないベクトルaが与えられたとき、直交座標系に関するa/‖a‖の成分（λ,μ）をaの方向余弦という。ここで、‖a‖は、aの長さを表す。したがってa/‖a‖は、a方向の単位ベクトルを表す。aがx軸、y軸となす角をそれぞれα、βとすれば
　　λ=cosα, μ=cosβ
でありλ²+μ²=1を満たす（図A）。また、空間にゼロでないベクトルaが与えられたとき、直交座標系に関するa/‖a‖の成分（λ,μ,ν）をaの方向余弦という。aがx軸、y軸、z軸となす角をそれぞれα、β、γとすれば
　　λ=cosα, μ=cosβ, ν=cosγ
でありλ²+μ²+ν²=1が成り立つ。平面上の直線に対するヘッセの標準形
　　λx+μy=p
や、空間の平面に対するヘッセの標準形
　　λx+μy+νz=p
における(λ,μ),(λ,μ,ν)は法線方向の方向余弦にほかならない（図B）。

［荻上紘一］

方向余弦説明図〔図A〕

方向余弦説明図〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

方向余弦【ほうこうよげん】

空間に直交座標系（x，y，z）があるとき，一つの有向直線がx，y，z軸の正の向きとはさむ角をそれぞれα，β，γとすると，l＝cos α，m＝cos β，n＝cos γをその直線の方向余弦という。これにより直線の方向が示され，またl²＋m²＋n²＝１の関係がある。→コサイン

出典　株式会社平凡社