解析幾何学（読み）カイセキキカガク（英語表記）analytical geometry

デジタル大辞泉

かいせき‐きかがく【解析幾何学】

図形の性質を、座標を導入することによって数式で記述し、代数的計算によって解析的に研究する幾何学。

出典　小学館

精選版 日本国語大辞典

かいせき‐きかがく【解析幾何学】

〘名〙 解析学の方法を用いて幾何学の図形を研究する数学の一部門。図形を、座標と呼ばれる一組の数を変数とする方程式で表わして分析し、その結果を幾何学的に解釈する。一七世紀、フランスのデカルト、フェルマーらによって始められた。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

解析幾何学 (かいせききかがく)
analytical geometry

幾何学は平面および空間における図形の性質を考察するが，この取扱いに二つの方法がある。一つはユークリッドによる古典的方法で，公理や公準と呼ばれる基礎の命題からはじめて論理的な論法で図形の性質を順次に証明していくという方法である。この際，数や代数学は用いられず，もっぱら図形が使用される。他の方法はP.deフェルマーやR.デカルトによって案出された方法で，平面や空間に座標を導入して，図形を数の間の関係によって表し，また逆に数の間の関係を図形で表現して，図形の問題を数の問題に翻訳し，代数の計算によって幾何の問題を処理するというものである。前者を総合幾何学または純粋幾何学というのに対し，後者を解析幾何学という。解析幾何学はデカルトにちなんでカルテシアンCartesian幾何学ともいわれ，また座標が基本となるので座標幾何学とも呼ばれる。なお，今日では微積分学などの極限を扱う数学をふつう解析学と呼んでいるが，微積分学の誕生以前には，解析とは発見的方法としての代数学を意味していたので解析幾何学の名がある。総合幾何学にあっては，定理を証明するに際し，図形に補助線などを加えることによって，すでに証明ずみの定理に結びつけるという手法が使われるが，これには個々の問題についてそれぞれのくふうがいり，きまった方法がない。これに対し，解析幾何学では幾何の問題は代数の問題に直されて機械的な計算で解ける。デカルトが解析幾何学の考えを述べたのは《方法叙説》（1637）の付録〈幾何学〉においてであったが，これの誕生には，F.ビエトらによってインド，アラビア伝来の代数学が整備されたことが貢献している。一方，解析幾何学の誕生は微積分学の形成に直接間接の影響を与えた。デカルト以後も解析幾何学はL.オイラーらによって発展し，ペルゲのアポロニオスらによる円錐曲線論も二次曲線論として代数的に整理された。さらに，平面や空間の点を2個または3個の実数の組として表す座標の考えを一般化することにより，n個の実数の組を点とみるn次元空間の概念が生まれ，解析幾何学はn次元空間の幾何学にまで一般化された。これにより幾何学の領域はおおいに広まるとともに，解析幾何学は幾何学における推論の道具としてばかりでなく，代数学や解析学における定理を示唆し理解することを助ける指導原理として機能することとなった。かくて数と図形とは本質的に別のものではなく，一方は他方の表現であるということが認識され，解析学，代数学，幾何学が有機的に結合した。

　次に，上述の解析幾何学の考え方を初等的な例について具体的に述べよう。平面上に，図1のように点Oで直交する2直線x′x，y′yを固定し，Oを原点，x′xを横軸，y′yを縦軸と呼ぶ。このとき，平面上の各点Pに対し，二つの実数x，yを次のように定義し，実数の組（x，y）を点Pの座標という。xはPから縦軸までへの距離に，Pが縦軸の右にあるか，左にあるかによって＋または－の符号をつけたものであり，yはxの定義においては“縦軸”を“横軸”に，“右”を“上”，“左”を“下”におきかえて定義されるものである。点Pの座標が（x，y）であることをP（x，y）で表す。どんな実数の組に対してもそれを座標とする点が一意的に定まる。このように座標を考えることにより，平面上の点と実数の組とが1対1に対応するが，この平面上の曲線（直線を含む）Γには，点P（x，y）がΓ上にあるための条件をxとyを用いて書き表した方程式が対応する。この方程式を曲線Γの方程式という。例えば，縦軸上の点H（0，h）を通り横軸となす角がθ°（－90＜θ＜90）であるような直線を考えるとき，点P（x，y）がこの直線上にあるための条件は（y－h）/x＝m（m＝tanθ°）であるから，直線の方程式はy＝mx＋hとなる（図2）。また，中心がC（a，b）で半径がrである円周を考えるとき，点P（x，y）がこの円周上にあるための条件は，ピタゴラスの定理により，（x－a）²＋（y－b）²＝r²となるから（図3），これが円周の方程式となる。幾何学的操作についても同じで代数的操作が対応する。例えば，二つの曲線の交点を求めるには，それらの曲線の方程式を連立させて解けば，その解が交点の座標となる。次に，具体例として，平面上で2定点A，Bからの距離の比が2：1であるような点の軌跡を解析幾何学により求めよう。このため，直線ABを横軸，線分ABの垂直2等分線を縦軸とする座標を考える。このとき，A（－a，0），B（a，0）と書け，P（x，y）からA，Bまでの距離の比が2：1であると，条件は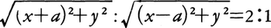，と表せる（図4）。これを計算すれば，

　（x－5/3a）²＋y²＝（4/3a）²

が得られるから，求める軌跡は（5/3a，0）を中心とし，半径4/3aの円周となる。ところで，この円周は直線ABと（a，0），（3a，0）で交わるが，これらの点は線分ABを2：1に内分および外分する点であるから，求める軌跡は，線分ABを2：1に内分および外分する点を直径の両端とする円周ということになる。
執筆者：中岡 稔

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

解析幾何学
かいせききかがく

座標系を用いて図形を数式で記述し、代数的計算によって古典幾何学の問題を処理する手法をいう。これは用いられる手法に対する名称であって、ユークリッド幾何学、リーマン幾何学、位相幾何学などのように幾何学の内容を表すものではなく、またそこで用いられる手法は主として線形代数学であるから「古典幾何学における代数的手法」というほうが適切である。解析幾何学は17世紀前半にR・デカルトによって始められ、平面または空間のユークリッド幾何学が考察の対象であったが、今日では広く古典幾何学一般が取扱いの対象とされる。しかし、普通に解析幾何学というときには、「ユークリッド幾何学における代数的手法」を意味することが多い。たとえば、二次元の場合には直交座標に関しては直線は一次方程式で表され、二次曲線（円、楕円(だえん)、双曲線、放物線）は二次方程式で表される。(x,y)を直交座標とするとき、2点(x1,y1)、(x2,y2)を通る直線の方程式は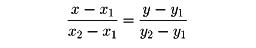

である。とくに2点(a,0)、(0,b)を通る直線は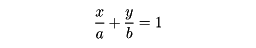

で表される（切片形）。中心が原点で、長軸、短軸が座標軸の方向に一致している楕円は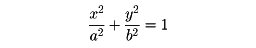

で表される。とくにa＝bならば円である。適当に座標変換（回転と平行移動）をすれば楕円の方程式はいつでもこの形（標準形）にすることができる。その際に用いられる代数的手法は二次形式の標準化（対称行列の固有値問題）である。双曲線、放物線についても同様である。三次元の場合には、直交座標に関して一次方程式で表される図形は平面であり、直線は連立一次方程式で表される。また、二次曲面（球面、楕円面、一葉双曲面、二葉双曲面など）は二次方程式で表される。

　一般にn個の実数の組(x1,x2,……,xn)全体の集合に対して2点(x1,x2,……,xn)、(y1,y2,……,yn)の間の距離を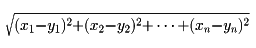

と定義することによって、n次元ユークリッド幾何学を代数的に構成することができる（n次元の解析幾何学）。ユークリッド幾何学以外の古典幾何学（非ユークリッド幾何学、アフィン幾何学、射影幾何学など）に対してもまったく同様に「～幾何学における代数的手法」がある。ただし、用いる座標系はそれぞれの幾何学で異なる。たとえばアフィン幾何学や射影幾何学では「直交」座標という概念は意味をもたない。すべての幾何学の問題に対して座標系を用いる代数的手法が最適であるとは限らない。座標を用いないで図形を直接考察する方法を、解析幾何学に対して総合幾何学または純粋幾何学という。

［荻上紘一］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

解析幾何学【かいせききかがく】

座標幾何学とも。座標を用いて図形を方程式で表し，代数的計算を行った結果を再び幾何学的に解釈することにより図形の性質を研究する幾何学。デカルト，フェルマーらが創始。→解析／解析学
→関連項目幾何学｜空間（数学）｜数学｜総合幾何学

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

解析幾何学
かいせききかがく
analytic geometry

(1) 曲線や立体のいろいろな性質を，解析的に，すなわち，簡潔な代数的記号を用い，座標系を導入して研究する分野。座標幾何学ともいわれる。 (2) 近年，代数幾何学に対して，それと類似の手法で解析的多様体の幾何学的性質を研究するのを，解析幾何学と呼ぶ用例がふえてきた。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の解析幾何学の言及

【幾何学】より

…天文学の影響を受けて，前150年ころにはヒッパルコスによって平面三角法および球面三角法がつくられ，前100年ころにはその発展に，三角形の面積の公式で有名なヘロンや，初等幾何学の定理に名の現れるメネラウスやプトレマイオス(トレミー)らが寄与した。
［解析幾何学］
　ユークリッドの幾何学はきわめて整然とした論理体系であるが，それはあくまで証明の科学であって発見のための科学とはいえない。また，その証明技術には統一的方法はなく，個々の場合についてそれぞれのくふうを必要とする。…

【座標】より

…直線，平面，空間における点に数または数の組を対応させて点の位置を表すしくみを座標系といい，点に対応する数または数の組をその点の座標という。座標を初めて考えたのはR.デカルトであり，彼はそれによって解析幾何学を創始し，幾何学的な図形を数の関係で表して幾何学を代数を用いて研究するという方法を開発したのである。この方法はその後に生まれた多くの幾何学の研究にも用いられ，それらに応じて各種の座標が導入された。…

【デカルト】より

…しかし同年のガリレイ断罪を知ってその発表を断念し，代りに《屈折光学》《気象学》《幾何学》の三つの〈試論〉に，序文として《方法叙説》を付けて37年に刊行した。このうち《幾何学》は幾何学と代数学を結合して解析幾何学を(フェルマーとともに)創始した業績として知られている。41年には形而上学の主著《省察》が，ホッブズ，アルノー，ガッサンディらの〈反論〉と著者の〈答弁〉を付けて刊行され，44年には自然学をも含むその体系のほぼ全容を示す《哲学の原理》が出版された。…

※「解析幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」