正弦定理（読み）セイゲンテイリ（英語表記）sine formula

デジタル大辞泉

せいげん‐ていり【正弦定理】

三角形の角と辺の関係を示す定理。平面上の三角形の頂点をA・B・C、対する辺をa・b・cとするとき、a/sinA＝b/sinB＝c/sinC＝2R（Rは外接円の半径）が成り立つというもの。正弦法則。

出典　小学館

精選版 日本国語大辞典

せいげん‐ていり【正弦定理】

1. 〘 名詞 〙 初等幾何学の定理の一つ。三角形の三辺とそれに対応する角の正弦の比がすべてその三角形の外接円の直径に等しいというもの。正弦法則。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

正弦定理 (せいげんていり)
sine formula

三角形ABCの辺BC，CA，ABの長さをa，b，cとし，この三角形の外接円の半径をRとすれば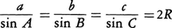，が成り立つ。これを正弦定理または正弦法則と呼んでいる。三角形の一つの辺とその両端の角がわかれば，この公式により他の2辺の長さが計算できるので，この公式は三角法において基本的である。球面三角形ABCについても，辺の長さの球の半径に対する比の値をa，b，cとすれば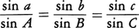，が成り立つ。これは球面三角法における一つの基本的な公式で，球面三角法における正弦定理または正弦法則と呼ばれている。
執筆者：中岡 稔

図－正弦定理

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

正弦定理【せいげんていり】

〈三角形ABCの頂角A，B，Cに対する辺の長さをa，b，c，外接円の半径をRとすると，（式１）の関係が成り立つ〉という法則。→余弦定理／三角法

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

正弦定理
せいげんていり

「正弦法則」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の正弦定理の言及

【平面三角法】より

…△ABCの内角A,B,Cの対辺の長さをそれぞれa,b,cとし，外接円の半径をRとするとき，公式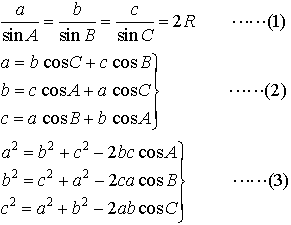，が成り立つ(図)。(1)は正弦定理，(2)は第1余弦定理，(3)は第2余弦定理と呼ばれる。これらの基本的公式より各種の公式が導かれるが，それらの中に，三角形の面積Sに関するヘロンの公式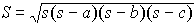，や，三角形の角をその3辺の長さから計算により求めるのに便利な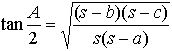，などの公式がある。…

※「正弦定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」