精選版 日本国語大辞典 「三角法」の意味・読み・例文・類語
さんかく‐ほう‥ハフ【三角法】
- 〘 名詞 〙
- ① 三角関数の性質や、その応用を研究する数学の一分科。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
- ② 第三角(第三象限)に物体をおいて製図する投影図法。第三画法。
日本大百科全書(ニッポニカ) 「三角法」の意味・わかりやすい解説
三角法
さんかくほう
直角三角形の辺の比によって決まる三角比を用いて、図形に関する計算をする方法。測量、航海、天文などの実用上の必要により、古くから発展した。大別して、平面上の問題を扱う平面三角法と、球面上の問題を扱う球面三角法に分かれるが、「球面三角法」は別項目で扱うので、ここでは平面三角法について説明する。
のような直角三角形において、次のように6種の三角比を定める。
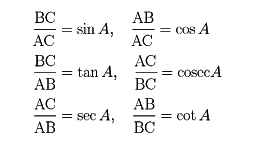
ここでは角が0゜<A<90゜と局限されている。これを一般角にまで拡張したものが三角関数である。三角形の性質を一般的に調べるためには、少なくとも鈍角に対してまで定義された関数値が必要である。以下では、三角比は三角関数として、すべての一般角について定義されているものとして扱う。いくつかの角については、三角比の値は、図形の性質を用いて容易に計算される()。
[竹之内脩]
正弦定理、余弦定理
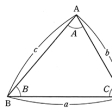
これらは計算の基礎となる定理である。いま、三角形ABCの三つの角の大きさをA、B、C、辺BC、CA、ABの長さをa、b、cで表す。これらを三角形の六要素という。三角形の性質を用いてにあげたような定理が成り立つ。このほか面積公式、ヘロンの公式、半角の正弦・余弦を表す公式もよく知られている。次のように、三角形ABCの六つの要素のうち適当な三つが与えられると、三角形の形状がそれによって定まり、他の三つの要素はそれらから計算される()。これを、三角形を解くという。三角測量は、この方法を継続して行っていくものである。
(1)2角と夾辺(きょうへん)が与えられている場合。角B、角Cとその間の辺aが与えられているとする。A=180゜-(B+C)であり、b、cは正弦定理の適用により求められる。
(2)2辺と夾角が与えられている場合。2辺b、cとその間の角Aが与えられているとする。第二余弦定理によりaの値が求められるから、次の3辺の場合に帰する。
(3)3辺が与えられている場合。3辺a、b、cが与えられると、半角の正弦、余弦を求める公式によって三つの角が求められる。
[竹之内脩]
三角法の歴史
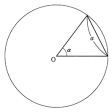
三角法の起源は古く、紀元前150年ころギリシアの天文学者ヒッパルコスにより円の角と弦の表がつくられたというが、現存しない。150年ころプトレマイオスは、円の中心角の大きさ0.5度おきに対応する弦の長さの表をつくった。これは、において、円の半径を1とするとa=2sin(α/2)であるから、正弦の表である。これは航海での実際上の必要性から研究が進み、その詳しい表が次々とつくられた。インド、アラビアにおける発展を経て12世紀ころからヨーロッパに再輸入された三角法は、さらに発展を続けた。15世紀末レギモンタヌスは、正弦、正接の詳細な表をつくり、また現代に至る形式を三角法に与え、その系統的展開を行った。正弦定理もこのなかに現れるが、余弦定理は16世紀末ビエタによって得られた。
[竹之内脩]
改訂新版 世界大百科事典 「三角法」の意味・わかりやすい解説
三角法 (さんかくほう)
trigonometry
平面または球面上の三角形ABCは三つの角A,B,Cと三つの辺a,b,cの6要素から成り立っているが,三角関数を用いると,これらの6要素の間のいろいろな関係式が得られる。例えば平面上の三角形については,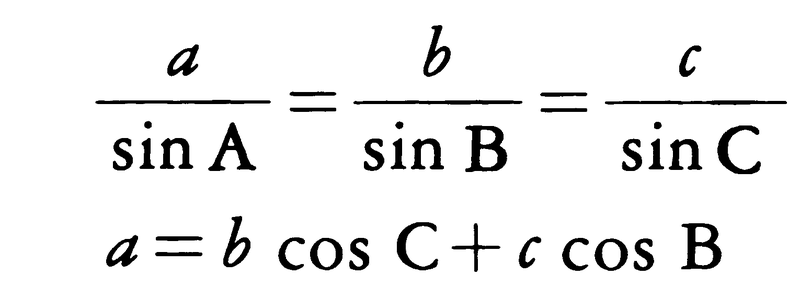
が成り立ち,球面上の三角形については,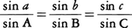
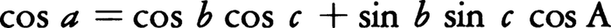
が成り立つ(図)。このような関係式を基本として,三角関数を応用することによって図形を研究するのが三角法である。対象が平面上の図形の場合には平面三角法,対象が球面上の図形の場合には球面三角法と呼ばれている。三角形の3要素を与えて残りの3要素を求めることを三角形を解くと呼ぶが,これは三角法における基本的問題である。三角法も元来この問題から起こったのであり,歴史的には天文学上の応用から始まったので,球面三角法のほうが平面三角法より先行した。古代のエジプト,バビロニア,中国にも三角法の芽生えが見られるが,前150年ころのギリシアのヒッパルコス(ニカエアの)が三角法の創始者といわれている。現在の三角法の形式はドイツのレギオモンタヌスRegiomontanus(1436-76)によるといわれ,その諸定理はJ.ネーピア,J.ケプラーを経て,L.オイラーに至って整備されたものである。三角法は天文学,航海術,測地法などに広く用いられている。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「三角法」の意味・わかりやすい解説
三角法【さんかくほう】
→関連項目アールヤバタ|球面三角法|視差|正弦定理|余弦定理
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「三角法」の意味・わかりやすい解説
三角法
さんかくほう
trigonometry
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の三角法の言及
【インド数学】より
…インド天文学にはメソポタミアやギリシアの天文学の影響が明瞭に認められるが,数学に関してはこれまでのところ決定的影響関係は見つかっていない。ただしインドの三角法の出発点はギリシアにあるとされている。しかし三角法はインドでも天文学の文脈で扱われるのが普通であり,伝統的数学(狭義のガニタ)の中に吸収されることはほとんどなかった。…
※「三角法」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...