球面三角法（読み）キュウメンサンカクホウ（英語表記）spherical trigonometry

デジタル大辞泉

きゅうめん‐さんかくほう〔キウメンサンカクハフ〕【球面三角法】

球面における距離や角を三角関数を利用して計算する方法。

出典　小学館

精選版 日本国語大辞典

きゅうめん‐さんかくほうキウメンサンカクハフ【球面三角法】

1. 〘 名詞 〙 三角関数を用いて、球面三角形の辺や角の関係を研究する数学の一分科。天文学や航海術、測量術などに応用される。⇔平面三角法。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

球面三角法 (きゅうめんさんかくほう)
spherical trigonometry

平面図形の研究に三角関数が応用されるが，球面上の図形についても同様である。前者を平面三角法といい，後者を球面三角法という。三角法は歴史的には天文学への応用から起こったため，平面三角法より球面三角法が先行した。その創始者はギリシアのヒッパルコスHipparchos（前150ころ）といわれており，メネラオスMenelaos（100ころ）もその発展におおいに寄与した。まず，球面三角形について述べよう。球面をその中心を通る平面で切ったときの切口の円を大円great circleといい，球面の一つの直径の両端の2点を対心点antipodal pointという。球面上の2点A，Bが対心点でなければ，A，Bを通る大円の周上においてAをBに結ぶ劣弧を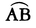で表す。これはA，Bにより一意的に定まる。球面上に3点A，B，Cがあり，これらは同一の大円の周上になく，いずれの二つも対心点でないとする。このとき，の作る球面上の図形を，球面三角形spherical triangle ABCといい，A，B，Cをその頂点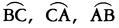，をその辺という。頂点Aにおいて辺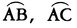に接する半直線のなす角を頂角Aといい，同様に頂角B，Cを定義する。平面上の三角形のときと同様，辺の長さをそれぞれa，b，cで表し，頂角A，B，Cの大きさを弧度法で測った量を同じくA，B，Cで表す。球面の半径がrならば，a/r，b/r，c/rは0とπの間の数で，それらの和は2πより小さい。A，B，Cはπより小さく，π＜A＋B＋C＜3πである。A＋B＋C－πを球面三角形ABCの球面過剰という。球面三角形ABCの面積は（A＋B＋C－π）r²で，3頂角によって定まる。したがって相似な球面三角形は合同となるが，球面三角形についても平面三角形の場合と同様の合同定理が成り立つので，球面三角形の3辺と3頂角の中の三つを与えれば残りのものが定まる。この求め方には3辺と3頂角の三角関数の間に成り立つ公式が用いられる。次にこれらの公式のおもなものをあげる。記述を簡単にするため以下では球面の半径は1とする。半径rの球面の場合にはa，b，cをa/r，b/r，c/rでおきかえればよい。まず，頂角Cが直角である球面三角形ABCでは次の公式が成り立つ。sin A＝sin a/sin c，sin B＝sin b/sin c，cos A＝tan b/tan c，cos B＝tan a/tan c，tan A＝tan a/sin b，tan B＝tan b/sin a，sin A＝cos B/cos b，sin B＝cos A/cos a，cos c＝cos a cos b，cos c＝cot A cot B。一般の球面三角形ABCについては，sin A：sin a＝sin B：sin b＝sin C：sin c（正弦公式）およびcos a＝cos b cos c＋sin b sin c cos A，cos b＝cos c cos a＋sin c sin a cos B，cos c＝cos a cos a cos b＋sin a sin b cos B，cos c＝cos a cos a cos b＋sin a sin b cos C（余弦公式）

が基本的である。

　これらの公式と三角関数の性質を用いれば，さらに多くの公式が求められる。例えば，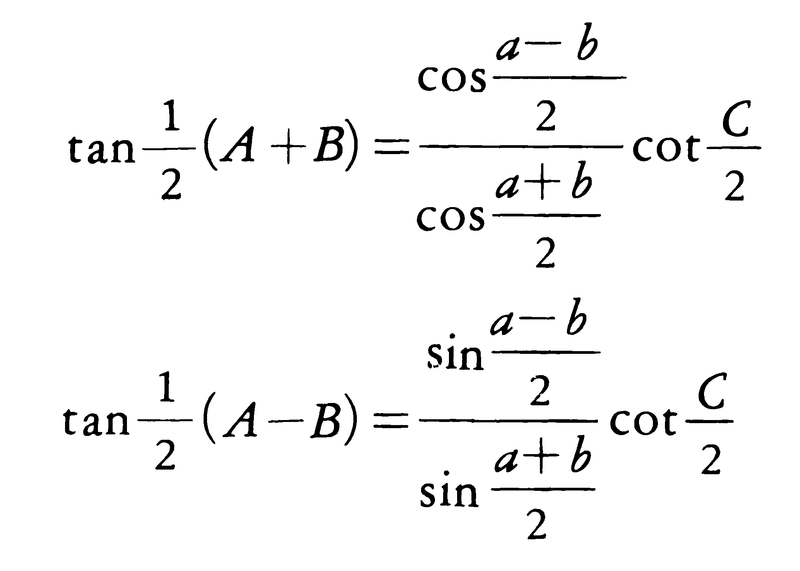

（ネーピアの公式）が成り立つ。球面三角形ABCの2辺a，bと頂角Cが与えられたとき，ネーピアの公式と正弦公式を用いれば，残りの2頂角A，Bと1辺cが求まる。球面三角形ABCの3頂角より3辺を求めるには，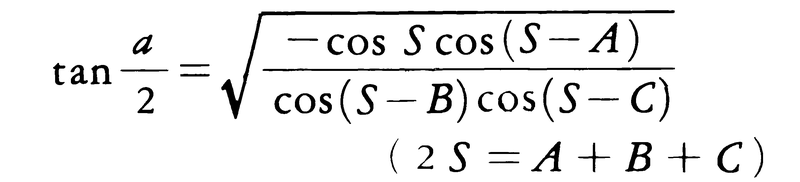

および同様の2式を用いればよい。球面三角法は航海術や天文学に広範に応用されている。
執筆者：中岡 稔

図－球面三角法

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

球面三角法
きゅうめんさんかくほう
spherical trigonometry

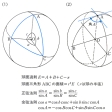
球面上の問題を解決するために三角関数を用いる計算法。地球上で応用して測量術、航海術、天球上で応用して天文学に用いられる。球をその中心Oを通る平面で切ったとき、球面上にできる切り口の曲線を大円といい、三つの大円の劣弧（大円を二分割したときの短いほうの弧）で囲まれる図形を球面三角形という（図の(1)）。この大円が交わる点を頂点（この場合三つありそれぞれA、B、Cとする）、頂点と頂点を結ぶ弧を辺という。中心Oと頂点A、B、Cを結ぶ半直線OB、OCのなす角aは、辺BCの長さと正比例するから、aは辺の長さを表す量とみなせる。同様に角b、cを定める。頂角Aは頂点Aにおける弧AB、ACへの接線の間の角として定められる。これは平面OAB、OACのなす角といっても同じことである（図の(2)）。同様に頂角B、Cを定める。いま
　　E=A+B+C-π
と置くと、つねにE＞0である。Eを球面過剰というが、球面三角形ABCの面積は球面過剰に比例する。つまり、球の半径をrとするとき、r²Eが面積である。

　このa、b、c、A、B、Cの間の関係を考えるのが球面三角法である。基本の関係として正弦法則、余弦法則がある。これらを用いて、球面三角形の辺、角の一部分がわかっているときに、他の辺、角を求めることができる。球面三角法は、航海などにおける必要から発達し、14、15世紀には今日に近い形ができあがった。

［竹之内脩］

球面三角法説明図〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

球面三角法
きゅうめんさんかくほう
spherical trigonometry

歴史的には天文学の研究に伴って起ったもので，球面三角形の角，辺の間にある関係を三角関数の諸法則を用いて考察し，その応用面をも研究する数学の一分野である。球面三角法を適用する空間図形のなかで基本的なものは，頂点を球の中心にもつ三面角である。この三面角の隣合う2面によってつくられる二面角 A，B，C は，三面角の3つの面と球面とが交わってできる球面三角形の角をつくる。いま A，B，C に相対する面角をそれぞれ α，β，γ とすれば，これら6つの角の間にはいくつかの基本的な関係がある。たとえば正弦公式: sin α/ sin A＝ sin β/ sin B＝ sin γ/ sin C ;正弦余弦公式: cos α＝ cos β cos γ＋ sin β sin γ cos A; cos A＝－ cos B cos C＋ sin B sin C cos α 。また球面三角形の面積 S は，球の半径を r とすれば，S＝Er² で与えられる。ただし，E は角 A，B，C をラジアンではかったときの角過剰 (A＋B＋C)－π である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

球面三角法【きゅうめんさんかくほう】

球面上の３点を大円の弧で結んでできる三角形を球面三角形といい，球面三角形の辺や角の関係を三角関数を使って数量的に算出し，またその応用を研究する数学の一分科を球面三角法という。天文学，航海術，測量等に利用される。→球／球冠／球面幾何学／三角法

出典　株式会社平凡社

世界大百科事典（旧版）内の球面三角法の言及

【三角法】より

…このような関係式を基本として，三角関数を応用することによって図形を研究するのが三角法である。対象が平面上の図形の場合には平面三角法，対象が球面上の図形の場合には球面三角法と呼ばれている。三角形の3要素を与えて残りの3要素を求めることを三角形を解くと呼ぶが，これは三角法における基本的問題である。…

※「球面三角法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」