等差数列（読み）トウサスウレツ

デジタル大辞泉

とうさ‐すうれつ【等差数列】

隣り合う二項の差が一定である数列。

出典　小学館

精選版 日本国語大辞典

とうさ‐すうれつ【等差数列】

1. 〘 名詞 〙 隣り合う各項の差がつねに一定であるような数列。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

等差数列
とうさすうれつ

ある数に、一定の数を次々に加えていってできる数列。算術数列ともいい、A. P.（arithmetic progression）と書くこともある。最初の数を初項、次々に加える一定数を公差という。初項をa、公差をdとするとき、その第n項a_nは、
　　a_n=a+(n-1)d
と表される。とくに、三つの数a₁,a₂,a₃が等差数列をなすとき、間の数a₂を等差中項という。等差中項は両端の数a₁、a₃の相加平均（算術平均）で表される。すなわち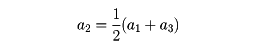

である。初項a、公差d、項数nの等差数列の和をS_nとすれば、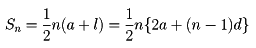

である。ここでlは、この数列の最後の項（末項という）を表す。とくに、奇数からなる数列1,3,5,……のn項の和はn²である。そして、一般項が項の番号nについての二次式であるような数列b₁,b₂,……すなわちb_n=An²+Bn+Cであるような数列については、その階差数列は等差数列であり、もしここでC=0ならば、b_nは、ある等差数列a₁,a₂,……に対して、そのn項目までの和を表す数列となる。数列a₁,a₂,……の逆数、すなわち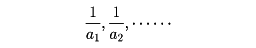

が等差数列をなすとき、a₁,a₂,……を調和数列という。とくに、三つの数a₁,a₂,a₃が調和数列をなすとき、a₂を調和中項という。これはa₁、a₃の調和平均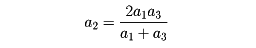

である。

［竹之内脩］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

等差数列 (とうさすうれつ)
arithmetic progression

例えば｛3，7，11，15，……｝や｛4，1，－2，－5，……｝のように，隣り合う2数の差が一定である数列を等差数列といい，その一定の差を公差という。上の二つの例では公差はそれぞれ4，－3である。初項（第1項）がa，公差がdである等差数列の第n項a_nはa_n＝a＋（n－1）dとなる。また，この等差数列の初項から第n項までの和S_nは，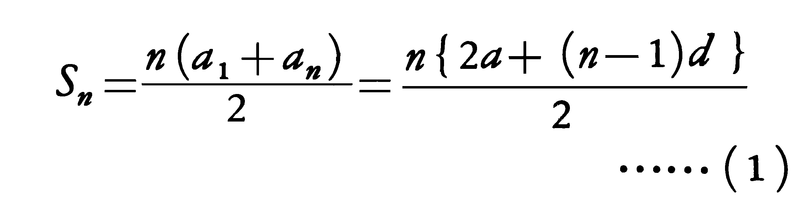

で与えられる。等差数列a₁，a₂，……，a_n，……の項の順に形式的に加号（＋）で結んだ式，

　a₁＋a₂＋……＋a_n＋……　……（2）

を等差級数arithmetic seriesというが，この無限個の項の和は初項も公差も0（すなわち，すべてのa_nが0）というつまらない場合を除き発散するから，（2）は具体的な意味をもたない。一般に（2）の形の級数の第1項から第n項までの和S_nを級数の部分和というが，等差数列の部分和の公式は（1）にほかならない。なお，等差数列そのもののことを等差級数，または算術級数ということがある。
→級数
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

等差数列
とうさすうれつ
arithmetic progression (sequence)

算術数列ともいう。たとえば，数列 1 ，3，5，7，9，…のように，数列 a₁ ，a₂ ，a₃ ，…，a_n ，…において，各数 a_n が，そのすぐ前の数 a_n-1 に一定数 d を加えることによって得られるとき，すなわち a_n＝a_n-1＋d を満たす数列であるとき，この数列を等差数列といい，AP と略記する。各数 a_n をこの数列の項，第1項 a₁ を初項，d ( ＝a_n－a_n-1 ) を公差という。また d＞0 ならば増加数列，d＜0 ならば減少数列になる。初項が a₁ ，公差が d の等差数列の，初項から第 n 項 a_n＝a₁＋(n－1)d までの和 S_n は，S_n＝(a₁＋a_n)・n/2＝na₁＋n(n－1)d/2 の公式で求められる。 S_n を単に等差数列の和ということもある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の等差数列の言及

【数列】より

…項の番号nに対応してa_nを定める規則が与えられれば，一つの数列が定義される。例えばa,d,rを定数とするとき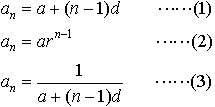，で定義される数列は，それぞれ等差数列，等比数列，調和数列と呼ばれる。また，a₁とa₂が与えられ，a_n＝1/2(a_n－1＋a_n－2)(n≧3)という規則が与えられれば，すべてのa_nが順次定まるから，一つの数列が定義される。…

※「等差数列」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」