反転（読み）ハンテン（英語表記）inversion

デジタル大辞泉

はん‐てん【反転】

［名］(スル)
１ ころぶこと。ひっくり返ること。また、ころがすこと。ひっくり返すこと。「マットの上でからだを反転する」「明暗が反転する」
２ 位置・方向・順序などが反対になること。また、反対にすること。「台風が進路を反転する」
３ 写真で、陰画を陽画に、また陽画を陰画にすること。「ポジをネガに反転する」
４ 数学で、平面上に中心O、半径rの円があるとき、O以外の任意の点Pをとり、半直線OP上にあってOP・OQ＝r² となるような点QをPに対応させること。→鏡像2
５ それまでとは反対の方向に回転すること。反回転。逆転。⇔正転。
[類語]横転・転倒・転覆・横倒し・将棋倒し・倒れる

出典　小学館

精選版 日本国語大辞典

はん‐てん【反転】

1. 〘 名詞 〙
2. ① ( 形動タリ ) ころがること。まろぶこと。また、ころがすこと。ころがすようにすること。また、そのさま。
   1. [初出の実例]「杜子美が百舌の詩にいひしは、またくここのうぐいす也。声反転として曲多しとか云し」(出典：随筆・胆大小心録（1808）八八)
3. ② ひっくりかえること。また、ひっくりかえすこと。
   1. [初出の実例]「此酒を飲けるに、忽渾身麻木(しびれ)てのけさまに倒れ、翻顛(ハンテン)して凳(しゃうぎ)の下におちたり」(出典：読本・忠臣水滸伝（1799‐1801）後)
4. ③ 物の位置・方向・順序等を反対にすること。また、反対になること。
   1. [初出の実例]「先進は質朴の方ぞ。さあれば此句と反転するほどに従がふと読ぞ」(出典：足利本論語抄（１６Ｃ）八佾第三)
5. ④ 数学で、中心がＯ、半径がｒの円でＯ以外の任意の点をＰとするとき、ＯＰを結ぶ直線上に OP・OQ=r² となるような点Ｑをとること。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
6. ⑤ 写真で、陽画を陰画に、またはその逆にすること。
7. ⑥ 高等飛行の一種。飛行機を迅速に半回転させ、さらに反回転させて反対の方向に飛行すること。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

反転
はんてん
inversion

数学用語、物理学用語、化学用語の三義がある。

［立花俊一］

数学

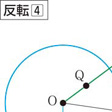
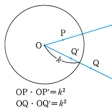
平面上で一つの円を考え、中心をO、半径をkとする。この円Oに関する反転とは、平面上の点Pに対して半直線OP上でOP・OP′＝k²となる点P′を対応させる対応をいう。円Oを反転円、Oを反転の中心、P′をPの反点という。また、Pが動いて一つの図形Fを描くとき、P′の描く図形F′をFの反形という。反転によって反転円の周上の各点は動かない。また反転円の内部と外部は入れ換わる。反転によって、点Oを通らない円はOを通らない円に、Oを通る円はOを通らない直線に、Oを通る直線は自分自身に移る。直線を半径無限大の円と考えれば、反転は円円対応ということができる。さらに、反転は共形対応（等角写像）であり、かつ円周上の4点の非調和比を不変にする（図A）。空間で考える場合は反転円のかわりに反転球を用いる。

［立花俊一］

物理学

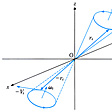
対象Aのあらゆる点につき、それぞれの位置ベクトルr_i＝(x_i,y_i,z_i)を－r_i＝(－x_i,－y_i,－z_i)に移してA′とする変換を能動的空間反転という（図B）。Aの各点の速度V_iもA′に移ると符号を変えるが、角運動量m_ir_i×V_iや角速度ω_iは変わらない。空間反転で符号が変わるベクトルを単にベクトル（あるいは極性ベクトル）といい、符号が変わらない量を擬ベクトル（あるいは軸性ベクトル）とよぶ。能動的変換に対して、直角座標軸の向きを三軸とも逆転させる数式表現上の変換を受動的空間反転という。これに対してもベクトルの極性と軸性の区別は引き継がれる。時間についても、物理現象Aを映画にとり、それを逆回しに映写して得る新しい物理現象A′に移ることを能動的時間反転という。これに対して数式表現上で時間軸の向きを過去に向け変える変換を受動的時間反転という。空間反転と時間反転をともに行うことを時空の反転とよぶ。物理学の基本法則を表す数式は小さい補正項を除いて受動的空間反転、時間反転で形が変わらず、したがって、現象Aがおこれば、それに能動的空間反転、時間反転を施して得る現象も物理法則を満たし、原理的には実現可能である。しかし、それが人間の手で実際に可能かどうかは別の問題である。

［江沢　洋］

化学

化学では、とくに有機立体化学の分野でよく使われ、(1)炭素原子Cの周りの立体配置が逆になる反転（インバージョンinversion）と、(2)シクロヘキサン環などの環反転（リングリバーサルring reversal）の2種類がある。

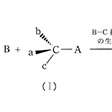
(1)炭素原子の立体配置の反転　脂肪族化合物の置換反応（S_N2反応）では、図Cにみるように、外部から試薬B（求核試薬）が中心原子Cを攻撃してきて、化合物（Ⅰ）の置換基Aと置き換わって化合物（Ⅲ）を生成する経路で進行する。この際に、反応中心のC原子の周りの置換基（図Cのa、b、c）の配置に反転がおこることがある。この反転は、初めに試薬Bが中心炭素原子Cに接近してB…C結合が生成して5配位炭素遷移状態（Ⅱ）になり、次にC…A結合が切れて、Bが接近してきたのと逆の方向にAが去っていくときに、他の置換基a、b、cは向きを変えないでとどまるので、結果として炭素原子Cの周りの立体配置は反転することになる。この反転はワルデン反転とよばれている。

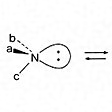
　これに似た反転が常温において容易におこる場合がある。たとえば、図Dのアンモニア、アミン類の窒素の周りでは炭素の場合と同じような立体配置の反転がおこる。しかし、この反転では結合の切断はなく非共有電子対（図Dの「：」）の向きが変わるだけなので、常温で速やかに反転をおこしている。

　糖類などの不斉(ふせい)炭素原子を多数もつ化合物で、一つの不斉炭素原子だけの立体配置を反転させる反応をエピマー化（エピ化）という。

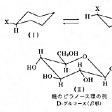
(2)シクロヘキサン環の反転　ある種の立体配座の変化を「反転」とよぶことがある。もっともよく知られている例は、シクロヘキサン環の反転で、図Eの一方のいす形（Ⅰ）と他のいす形（Ⅱ）との間で反転運動をしていることが知られている。この反転は、環を形成しているC-C結合の周りの回転によりおこり、環を構成するC-C結合の切断を必要としないので、常温で速やかにおこっている。この反転により環についている水素（H）や置換基（X）の向きが変わる。

　シクロヘキサン環のような飽和非平面構造の環炭素原子は、環の平面方向に伸びているエクアトリアル結合（赤道結合）と垂直方向に伸びているアキシアル結合（軸結合、極結合）をもっている。図Eの（Ⅰ）ではC-X結合はエクアトリアル、（Ⅱ）ではC-X結合はアキシアルである。シクロヘキサン環が（Ⅰ）から（Ⅱ）に反転すると、C-X結合はエクアトリアからアキシアルに、C-H結合はアキシアルからエクアトリアルに変わっている。

　図E（Ⅲ）の下段はD-グルコースの構造式である。糖類の基本骨格であるピラノース環はシクロヘキサン環の一つの炭素原子を酸素に置き換えたピラノース環構造をもっている。ここでも環の反転がおこっていて、置換基の向きが生物活性などの性質に大きな影響を及ぼす例が知られている。

［廣田　穰　2015年3月19日］

『坪井忠二他著『右と左――対称と非対称の世界』（1981・サイエンス社）』

[参照項目] | シクロヘキサン | 非調和比

反転〔図A〕

能動的空間反転〔図B〕

脂肪族化合物の反転〔図C〕

アンモニアやアミン類の反転〔図D〕

シクロヘキサンの反転〔図E〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

反転
はんてん

(1) reversal　輝線スペクトルが低温気体の存在によってスペクトル線の中心部で吸収を受け，暗くなること。反彩ともいう。ナトリウムのD線による炎色反応スペクトルは反転することが多い。太陽スペクトルにおけるフラウンホーファー線もこの例である。 (2) reversal　写真の陽画を陰画に，また陰画を陽画に変えること。 (3) inversion　ベクトル空間の元 (ベクトル) の成分の正負の符号をすべて逆にする変換。座標変換の場合は，座標成分の符号がすべて逆になる。座標軸を固定して考える場合は，原点に関して点対称な変換に相当する。物理学では，空間座標 x，y，z を －x，－y，－z に変え，時間座標 t を変えない変換を空間反転，時間座標だけ符号を変える変換を時間反転という。 (4) inversion　ある立体配置が，それに対応する逆の立体配置に変化すること。 (→ワルデン反転 ) (5) inversion　半径 a の円の中心から r の距離にある点を，同じ半径上で rr'＝a² を満たす距離 r' に移すこと。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

反転 (はんてん)
inversion

平面上にOを中心としrを半径とする円があるとき，この平面上のO以外の各点Pに対し，半直線OP上に点P′をOP・OP′＝r²であるようにとって，PをP′にうつす対応を反転という。このときOを反転の中心，rを反転の半径という。上では中心Oの像は定義されていないが，PがOに近づくときP′はどんどん遠くへいくので，平面に一つの無限遠点をつけ加えて，Oは反転により無限遠点にうつるとすれば，反転は一つの無限遠点をつけ加えた平面からそれ自身の上への1対1対応となる。直線および円の反転による像は直線，または円で，交わる2曲線は反転によって同じ大きさで交わる2曲線にうつされる。空間に球があるとき，空間における反転が平面上のときと同様に定義され，同様の性質が成り立つ。
執筆者：中岡 稔

図－反転

出典　株式会社平凡社「改訂新版　世界大百科事典」

化学辞典 第2版

反転
ハンテン
inversion

原点Oに対して，ある図形A内のすべての点(x，y，z)を点(－x，－y，－z)に移して図形A′をつくる操作．その原点を反転中心，対称心または対称中心という．2回の反転によって図形が完全にもとの図形と重なるとき，その図形は対称心をもつという．

出典　森北出版「化学辞典（第2版）」

ASCII.jpデジタル用語辞典

反転

入力した文字列を変換するときや、文字列を選択するときなどに、ディスプレイ上で文字列の周りに色が付くこと。反転することによって、ユーザーの注意を引ける。

出典　ASCII.jpデジタル用語辞典

世界大百科事典（旧版）内の反転の言及

【国際私法】より

…もし，このイギリス人が日本に住所をもつと認められるならば，いったいどちらの国法を準拠とすべきかが疑問となろう。問題を本国に送り込み(送致Verweisung)その解決するところにゆだねたものの，本国では逆にそれを日本に送り返してきた(反転あるいは反対送致)という事態である。すなわち抵触法自体が内外で抵触している情況である。…

【性倒錯】より

…異常性欲のうちで，性欲の質的な異常を性倒錯という。これをさらに，(1)性対象の異常であるインバージョンinversion，(2)性目標の異常である狭義の性倒錯，の二つに分けるのが普通である。歴史的に性対象の異常とされてきたものには，以下の行為がある。…

【突然変異】より

…
［染色体突然変異］
　これは元来，光学顕微鏡で観察できる染色体の構造変化，たとえば体細胞分裂中期の染色体の形態，減数分裂中期の染色体対合の状態，ショウジョウバエの唾腺（だせん）染色体のような巨大染色体の縞模様などによって解析されるものを指したが，現在では遺伝解析，電子顕微鏡観察，化学分析などによって検出できる微小なものも含めるようになっている。その中には，染色体の一部(末端部分の場合も中間部分の場合もある)が消失した欠失deletion，染色体の一部が同一染色体の別の場所または別の染色体に移った転座translocation，染色体の一部が本来の場所に隣接または別の場所に付け加わった重複duplication，染色体の一部の方向性が逆になった逆位inversionなどがある(図2)。いずれも染色体の切断‐再結合および不等組換え，非相同染色体組換えなどの異常組換えによって生じると考えられている(図3)。…

※「反転」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」