比熱（読み）ヒネツ（英語表記）specific heat

デジタル大辞泉

ひ‐ねつ【比熱】

物質1グラムの温度をセ氏1度上げるのに必要な熱量。圧力一定のときを定圧比熱、体積一定のときを定積比熱という。比熱容量。

出典　小学館

精選版 日本国語大辞典

ひ‐ねつ【比熱】

1. 〘 名詞 〙 ある物質一グラムの温度を摂氏一度上げるのに要する熱量。特に気体では体積を一定にしたとき、または圧力を一定にしたときの比熱をそれぞれ定積比熱・定圧比熱という。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

比熱
ひねつ
specific heat

1グラムの物質の温度を1K上げるのに必要な熱量。より一般的には、ある一定量の物質を1K上げるのに必要な熱量のことを熱容量heat capacityという。比熱にその物質のグラム数を乗じたものに等しい。すなわちmグラムの物質の熱容量をC、この物質の比熱をcとすると、C＝mcである。本項では熱容量を中心として記述する。

　水1グラムの温度を1K（厳密には1気圧下で14.5℃から15.5℃）上げるのに必要な熱量は1カロリー（これが実はカロリーcalorie〈略号cal〉の定義）であるから、熱量の単位をカロリーととると、水の比熱は1である。物質の比熱はほとんどいつもこのように、カロリー／（グラム・度）で表される（cal/g・Kあるいはcal・g^-1K^-1である）。純物質あるいは気体に対しては1モル（分子量にグラムをつけた量）に対する熱容量を用いることが多く、これをモル比熱molar heatまたは分子熱molecular heatという。1モルをMとすると分子熱C^Mは、C^M＝M_cで与えられる（元素の場合には、これは原子熱とよばれる）。

　機械、装置などに使用されている材料の比熱が、それらの性能に関係することも少なくない。また、水の比熱が非常に大きいことが、海洋に近い地域の気候を温和にしていることはよく知られたことである。一方、比熱という量は原子論的にも比較的議論しやすいものであって、物性論におけるいろいろの理論の正当性を判断するのに、比熱の理論値と実験値とがどの程度あうかということが、有用な判定資料になることが多い。

　熱容量は、物質の温度を変えるときの条件によって異なる。よく関心がもたれるのは、外からの圧力が一定に保たれる場合の熱容量すなわち定圧熱容量heat capacity at constant pressure（記号C_P）と、試料の体積が一定に保たれる場合の熱容量すなわち定積熱容量heat capacity at constant volume（記号C_V）との差異である。直接に測定できるものは定圧熱容量である。

［沢田正三］

比熱の値

金属の定圧比熱は0.03～0.2cal/g・K程度で、水の1に比しては相当小さい。これが金属が「熱しやすく冷めやすい」ゆえんである。一方、水素ガスは室温で3.4と大きい。いずれにしても物質の比熱は、電気伝導率などのように物質の種類によって著しく差異のあるような物性量ではない。

［沢田正三］

熱容量の熱力学的表式

物質に外部から微小な熱量d'Qが加えられて、物質の温度がTからT＋dTに変化するとき、物質の熱容量Cは定義によりC＝d'Q／dTで与えられる。一方、熱力学第一法則により、等方性物質ではdU＝d'Q－pdVが成り立つ。ここでU、p、Vはそれぞれ内部エネルギー、圧力、体積である。したがって定積熱容量はC_V＝(∂U/∂T)^Vで与えられる。また、定圧熱容量はC_P＝(∂H/∂T)^Pで与えられる。Hはエンタルピーとよばれ、Uと同じく一つの熱力学的ポテンシャル（あるいは熱力学的関数）であって、H＝U＋pVで表される。定圧熱容量と定積熱容量との差は一般にはC_P－C_V＝TVα²/κ^Tで与えられる。ここにα＝(1/V)(∂V/∂T)^Pは体熱膨張率、κ^T＝－(1/V)(∂V/∂p)^Tは等温圧縮率である。つねにC_P＞C_Vであって、その比すなわちγ＝C_P/C_V＞1は気体ではとくに重要な物質定数である。理想気体ではその状態方程式pV＝n_mRT（n_mはモル数、Rは気体定数）から、C_P－C_V＝n_mRであることが容易にわかる。

［沢田正三］

熱容量の原子論的表式

(1)理想気体　気体ではそれを構成する分子が、現在の温度に相当する熱エネルギーをもって、ほとんど自由にこの気体の容器が占めている全空間を飛び回っている。これらの分子の運動のようすは古典力学（ニュートン力学）で十分取り扱える。たとえば、気体の圧力は、分子が容器の壁に衝突して跳ね返るときの運動量の変化に対応する力である。とくに理想気体は、分子の大きさを無視することができ、かつ分子の間の相互作用（すなわちポテンシャルエネルギー）がまったくないものである。この場合には、分子1個のもつエネルギー（運動エネルギーだけ）εはε＝(3/2)kTで与えられることがすぐいえる。ここに、k＝R/N_Aはボルツマン定数とよばれるたいへん重要な基本定数であり、N_Aはアボガドロ定数、すなわち物質1モル中の分子の数である。理想気体の1個の分子の運動の自由度は3であるから、先のεの式は、各自由度当りの運動エネルギーは(1/2)kTであることを示す。この法則はエネルギー等分配則とよばれる。

　理想気体の定積分子熱容量C_V^Mは以上のことからすぐにC_V^M＝3/2Rであることがいえる。また前述の定圧熱容量と定積熱容量の関係式から、C_P^M＝5/2Rが得られる。R＝1.987cal/g・Kであるから、定圧分子熱容量C_P^Mの理論値は4.97cal/g・Kである。一方、たとえば、アルゴンガスの定圧比熱の実測値は、室温で0.124cal/g・Kであるから、分子量39.95を用いてC_P^Mの実測値は4.95cal/mol・Kであって、この両者はよく一致する。さらに定圧比熱と定積比熱の比γの理論値は5/3＝1.67であるが、実測値も1.67である。アルゴンガスのような不活性ガスでは、分子は原子そのもので、分子の自由度は確かに3であるから、この結果は十分予測できる。ところが、N₂やCO₂のような多原子分子気体でも、分子の並進の自由度のほかに回転の自由度を考慮すると、C_P^M、γの理論値と実測値とがやはりよく一致する。これらのことは、気体はほとんど自由に飛び回っている分子の集まりであるとする以上の考え方がまことに妥当であることを示すものである。

(2)固体　固体の室温付近の比熱の実測値に関しては、固体の分子熱容量が固体の種類に無関係に、約6acal/mol・Kであるというデュロン‐プチの法則（1819）がよく当てはまる。aは、分子中の原子の数であり、たとえばCuでは1、NaClでは2である。この法則は、理想気体のところで述べた運動エネルギーに関する等配則の拡張されたもので容易に説明できる。拡張則は、運動エネルギーのほかにポテンシャルエネルギーが存在する場合には、1自由度当りのエネルギーはkTであるということである。固体は原子が規則正しく格子状に配列したものであるが、各原子はその平衡位置の周りで現在の温度Tに相当する熱エネルギーをもって振動（これは格子振動といわれる）をしている。振動は、一般に運動エネルギーと位置のエネルギーとの消長でおこるものであるから、1自由度当りのエネルギーはkTである。原子1個の自由度は3であるから、原子1個当りのエネルギーは3kTであり、1モル当りでは3aRTで、分子熱容量は3aR≈6acal/mol・Kなのである。

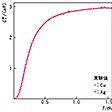
　デュロン‐プチの法則は、実は室温付近の狭い温度範囲でしか成立しない。比熱は、温度降下とともに減少し、絶対零度付近では急激に0に近づく。比熱の低温におけるこのような顕著な温度依存性は、古典物理学の範囲内では説明できず、量子論によって初めて説明できた。すなわち、振動している原子は調和振動子と考えてよいが、そのとりうるエネルギーが、古典論では連続的なのに対して、量子論では3nhν（n＝0,1,2,……）のようにとびとびである。ここに、νは振動数であり、hはプランク定数とよばれ、量子論におけるもっとも重要な基本定数である。このエネルギー準位の離散性のために、比熱が低温で著しく減少することが統計力学で明瞭(めいりょう)に示される。

［沢田正三］

異常比熱

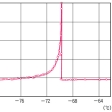
物質の比熱は、温度上昇とともに、普通は単調に増加する。ところが、リン酸二重水素カリウムのように、比熱が異常な温度依存性を示すことも少なくはない。このような比熱は、異常比熱anomalous specific heatといわれ、ほとんど相転移に伴っておこる。相転移とは、ある物質の性質が、その物質に特有な温度（転移点）を境として急に変化する現象である。強磁性、強誘電性、超伝導性などの物質の特異な性質は相転移に伴って現れるので、相転移は基礎分野でも応用分野でも大いに関心がもたれる現象である。

［沢田正三］

『沢田正三・影山誠三郎・小口武彦・柳武敏著『基礎物理2』（1973・槇書店）』

[参照項目] | エネルギー等分配則 | 気体分子運動論 | 原子熱 | 相転移

普通の温度依存性

異常な温度依存性（異常比熱）

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

比熱 (ひねつ)
specific heat

単位質量の物質の温度を単位温度だけ上げるのに必要な熱量。水のように比熱の大きいものは温まりにくく，冷めにくい。逆に比熱の小さいものは温まりやすく冷めやすい。比熱の単位としては通常，1gの物質を1K上げるのに要する熱量をcalで表したもの，すなわちcal/K・gが使われる。比熱と物質の質量との積を熱容量といい，気体に対しては，1molに対する熱容量を用いることが多く，これをモル比熱molar heatという。

　比熱は同じ物質でも温度や圧力によって異なり，とくに物質の状態が気体，液体，固体であるかによって大きく異なる。また熱の加え方によっても差を生じ，一定圧力のもとで温度を上げるときの比熱を定圧比熱，一定体積のもとで温度を上げるときの比熱を定積（容）比熱という。定圧比熱をc_P，定積比熱をc_vとすると，一般にc_P＞c_vであるが，それは，圧力一定で温度を上げると，一般に体積が膨張し，その分だけ余分に熱を必要とするからで，0～4℃の水のように温度が上がると体積が減少する場合はc_v＞c_Pとなる。気体では，温度上昇による体積の膨張が著しいので，c_Pとc_vの差は非常に大きく，理想気体の場合，

　c_P－c_v＝R/m

の関係がある。ここで，Rは気体定数，mは気体の分子量である。液体や固体では，体膨張係数が気体に比べてはるかに小さいので，定圧比熱と定積比熱との差は非常に小さく，定積比熱の数%の程度である。

　ミクロに比熱を見ると次のように解釈できる。温度を上げるために熱を物質に与えると，物質を構成している分子や原子の熱運動がより激しくなり，その運動エネルギーも増加する。それに必要なエネルギーが比熱にほかならない。

　気体のモル比熱は分子の構造によって決まる。アルゴンなどの単原子気体では定積モル比熱C_vは3/2R，水素，酸素などの2原子気体ではC_v＝5/2R，多原子気体ではC_v＝3Rに近い。

　固体の比熱に関しては，その定積モル比熱C_vが3Rに等しいというデュロン=プティの法則や，アインシュタインによるアインシュタインの比熱式，これを改良したデバイによるデバイの比熱式がある。デバイの比熱式は，格子振動を連続体の弾性振動（縦波と二つの横波）でおきかえることによって導かれたもので，絶対温度をTとして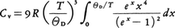，と表される。ここでΘ_Dはデバイの特性温度と呼ばれるパラメーターであり，このデバイ温度に相当するエネルギーをもつ振動によって，比熱は，ほとんど決定される。ちなみに前の式でT＝Θ_Dとおくと，C_vは，ほとんど高温の極限3Rに近くなる。

　相転移点，とくに二次相転移点の近傍では，比熱が異常に大きくなることが多い。これを異常比熱といい，臨界現象の研究にとっては非常に重要な現象である。すなわち，この異常比熱の測定により，二次相転移の存在およびその転移点を確証することが多い。
執筆者：鈴木 増雄

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

比熱
ひねつ
specific heat

単位質量の物質の温度を単位温度だけ上昇させるのに必要な熱量。SI単位系では物質 1kg を温度 1K上げるのに要する熱量をジュール単位で表示する。すなわち，単位は J/（kg・K）となる。比熱は温度によって変化し，その温度変化の研究は量子論の発展に寄与した。温度を上げるときの条件によっても比熱は異なり，体積一定のときの定積比熱 c_v（定容比熱ともいう）に比べ，圧力一定のときの定圧比熱 c_p は体積を増加させるのに必要な仕事に相当する熱量だけ大きい。両比熱の差は，気体では熱膨張が大きいから常温で c_v の数十%もあるが，液体や固体では常温で 10%以下，約－200℃以下の低温では c_p≒c_v である。比熱は熱量計を用いて測定され，また定速で加熱したときの試料の温度変化率から算出される。気体では c_p も c_v も直接に測定できるが，液体や固体では c_p だけが測定でき，c_v は熱力学により導き出した式から算出される。つまり T を絶対温度，d を密度，αを体膨張率，κを圧縮率とすると，c_p－c_v＝Tα²/κd である。特に理想気体では，前式はマイアーの関係式c_p－c_v＝R/m（R は気体定数，m は分子量）となる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

比熱【ひねつ】

物体の単位質量当りの熱容量。つまり物質1g（または1mol）の温度を1K上げるのに要する熱量。単位はJ/K・g，cal/K・g（または，J/K・mol）。なお，1molに対する比熱をモル比熱という。一般に温度によって多少変わる。加熱の際圧力を一定に保ったときの比熱を定圧比熱C(/p)，体積を一定に保ったときの比熱を定容（積）比熱C(/v)といい，固体や液体では両者の差はごく小さいが気体では大きく，理想気体ではC(/p)−C(/v)＝R/M（Rは気体定数，Mは気体の分子量），C(/p)/C(/v)＝1.67（１原子分子の場合），C(/p)/C(/v)＝1.4（２原子分子の場合）となる。
→関連項目原子熱｜断熱変化｜定積比熱｜熱量計

出典　株式会社平凡社

栄養・生化学辞典

比熱

　単位質量の物質の温度を単位温度だけ上昇させるのに必要な熱量で，通常水を基準とし，それに対する比率で示す．

出典　朝倉書店

化学辞典 第2版

比熱
ヒネツ
specific heat

[同義異語]比熱容量

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内の比熱の言及

【デバイの比熱式】より

…固体の比熱について，アインシュタインの比熱式の改良としてP.デバイが1912年に提案した式。アインシュタインは，固体内の個々の格子点を独立な単振子として扱ったが，デバイは格子の集団運動の本質をとり入れて，まず固体を連続弾性体とみなした。…

【デュロン=プティの法則】より

…デュロンPierre Louis Dulong(1785‐1838)とプティAlexis Thérèse Petit(1791‐1820)によって1819年に発見された，固体の定積モル比熱C_vについての経験法則。固体が何であるかによらずC_v＝3R(Rは気体定数)であるとする。…

【熱】より

…物質によって同じ量を同じ温度上げるのに必要な熱量が異なることを示したのである。ブラックの研究に刺激されたA.L.ラボアジエは，P.S.ラプラスと協力して比熱の精密な測定を行った。ブラックらの研究によって初めて熱の量が測定される量として把握されたのである。…

【熱容量】より

…また，熱容量の大きい物質ほど冷えにくい。一様な物質の場合には，単位質量当りの熱容量を比熱という。したがって，熱容量は比熱と質量の積で与えられる。…

※「比熱」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」