パスカルの三角形（読み）パスカルのさんかっけい（その他表記）Pascal's triangle

精選版 日本国語大辞典

パスカル の 三角形(さんかっけい)

1. 二項係数を三角形状に配列したもの。二項係数を具体的に計算するのに用いる。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

パスカルの三角形 (パスカルのさんかくけい)
Pascal's triangle

図1のような三角形状の数の配列をパスカルの三角形という。パスカルの三角形の構成方法を説明するために，次のような記号を導入しよう。上から第n行目，左から第r番目の数をa₍_n,r₎と表す。nは負でない整数，rは0からnまでの整数の範囲を動く。図2は，このa₍_n,r₎を並べたものである。パスカルの三角形は，次の規則（1），（2）に従って構成される数の配列である。

（1）すべてのnに対して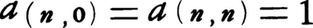，が成り立つ。

（2）すべてのn，rに対して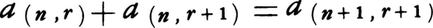，が成り立つ。

　パスカルの論文《数三角形論》（執筆1654）の中でこの三角形について詳しい議論が展開されている。パスカルの時代は，記号の使用法が未発達であり，彼はa₍_n,r₎にあたる数を記号を用いて表現していないが，たとえば，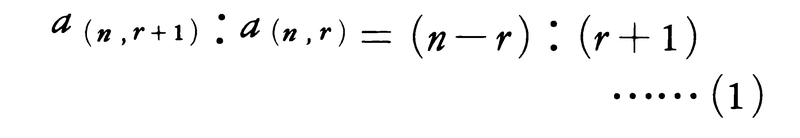

が成り立つこと，および〈a₍_n,r₎はn個のものからr個のものを同時に選ぶ組合せの数に等しい〉に相当する命題を，nについての数学的帰納法を用いて証明している。これは，数学史上画期的な事柄であるとされている。数学は，ここで数学的帰納法により初めて〈すべての自然数〉についての命題をもちうるようになったからである。

　上記の命題（1）から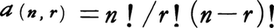が導かれる。通常，a₍_n,r₎は記号_nC_rまたは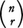を用いて表される。_nC_rの意味を考慮すると，二項定理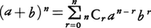，の成り立つことがわかる。
執筆者：清水 昭信

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

パスカルの三角形
パスカルのさんかくけい
Pascal's triangle

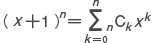二項展開の係数を三角形状に並べたもの。ここで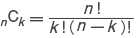，であり，これは n 個から k 個を選ぶ組み合わせの数を表す（→組合せ論）。パスカルの三角形では，それぞれの段の右端と左端は 1であり，隣り合う二つの数の和として，それらの数の間にある一つ下の段の数が得られる。これは等式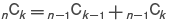に基づいている。また，次のようないくつかの性質をもつ。(1) m 段目の数の 2乗和は，2m－1段目の中央の数になる。(2) 奇数段目の中央の数字からその二つ隣の数を引くと，カタラン数になる。ここで，n 番目のカタラン数は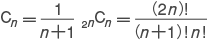で与えられる。たとえば，9段目の中央の 70からその二つ横の 28を引くと 42であり，これは 5番目のカタラン数に等しい。パスカルの三角形の名称は，フランスの数学者ブレーズ・パスカルにちなむ。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

パスカルの三角形【Pascal's triangle】

二項係数を次々に並べてつくられる三角形状の配列．

出典　朝倉書店

世界大百科事典（旧版）内のパスカルの三角形の言及

【中国数学】より

…朱世傑はまた《四元玉鑑》(1303)を著し，四元による計算法を説いたが，この書には級数の和を求める問題が多く含まれ，また(a＋b)ⁿを展開した時の係数を表示した図がある。これは17世紀のフランス人哲学者パスカルにちなんで〈パスカルの三角形〉と呼ばれるものに一致する。　南宋治下の数学者には，秦九韶および楊輝が有名である。…

【二項定理】より

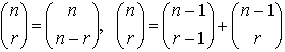…これより，(a＋b)^n－1の展開における第r項と第r＋1項との係数の和は，(a＋b)ⁿの展開における第r＋1項の係数に等しいことがわかる。これら二項係数を順々に並べて書いた図形をパスカルの三角形という。【杉江 徹】。…

※「パスカルの三角形」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」