改訂新版 世界大百科事典 「フィボナッチ数」の意味・わかりやすい解説
フィボナッチ数 (フィボナッチすう)
Fibonacci sequence
漸化式u0＝0，u1＝1，……，un＝un-1＋un-2（n＝2，3，4，……）で定まる数列｛un｝をフィボナッチ数列，各項をフィボナッチ数という。u2＝1，u3＝2，u4＝3，u5＝5，u6＝8，u7＝13，u8＝21，u9＝34，u10＝55である。フィボナッチ，通称ピサのレオナルドは1202年《アバクスの書Liber abaci》を著し，アラビア数字と四則の筆算を取り扱い，ヨーロッパの数学に大きな影響を与えた。この本の中の問題の一つに上述の漸化式に関係するものがあり，それにちなんでフィボナッチ数と名付けられた。フィボナッチ数unは定義によりn≧1のとき正の整数であるが，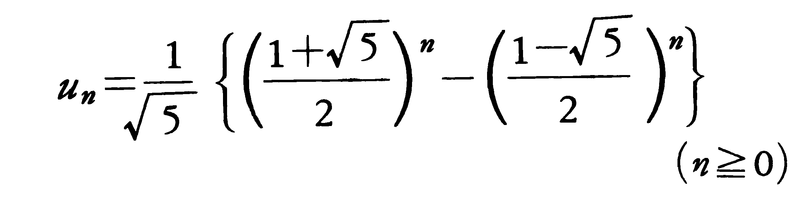
と表示することができる。ここに現れる2数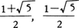
は互いに逆数であり，黄金分割の比としても現れる。また，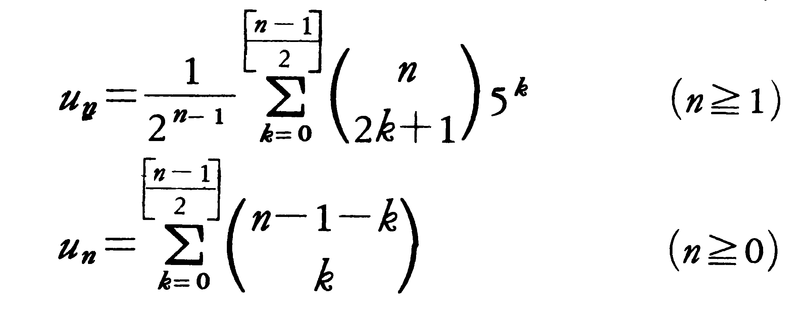
とも表示できる。ここで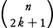
などは二項係数を，
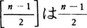を超えない最大の整数を表す。θが
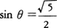を満たせば，
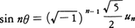である。フィボナッチ数の間には種々の関係式が知られている。例えば，
u1＋u2＋……＋un＝un+2－1
u12＋u22＋……＋un2＝unun+1
u13＋u23＋……＋un3＝1/10（u3n+2＋（－1）n⁺16un-1＋5）
mとnの最大公約数がdであれば，umとunの最大公約数はudである。また平方数であるようなフィボナッチ数は1と144のみである。フィボナッチ数はヒマワリやマツの実の種子の配列など，自然界にしばしば見られる。
執筆者：上野 健爾
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報