四則（読み）シソク（英語表記）arithmetic operations

デジタル大辞泉

し‐そく【四則】

足し算・引き算・掛け算・割り算の四つの算法。加・減・乗・除。また、これを用いてする計算。

出典　小学館

精選版 日本国語大辞典

し‐そく【四則】

1. 〘 名詞 〙 ＝しそくざん（四則算）〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

四則 (しそく)
arithmetic operations

分数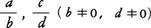の間では，次のような演算ができる。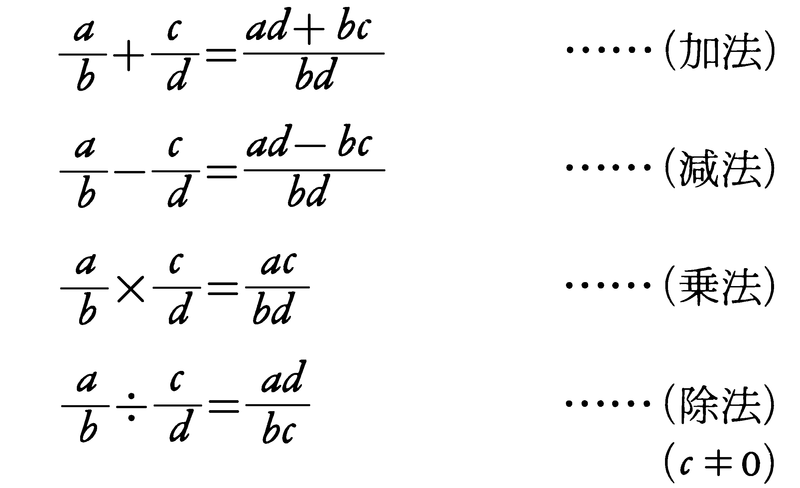

この和，差，積，商を得る4種類の基本的演算，加法，減法，乗法，除法を四則演算という。ただし，除法では0で割ることは考えない。四則演算は有理数どうしに限らず，二つの実数や複素数の間でも可能である。一方，二つの整数の和，差，積は整数であるので，整数の範囲内で，加法，減法，乗法は可能であるが，7÷8のように，商はかならずしも整数とはならず，除法は可能とは限らない。また，二つの自然数の和，積は自然数であるが，29－33のように，差はかならずしも自然数とはならず，自然数の範囲内では減法も可能とは限らない。一般に，四則演算が可能な集合を体という。上の例では，有理数の集合，実数の集合や複素数の集合は体であるが，整数の集合や自然数の集合は体ではない。

　ところで，四つの演算のうち，加法と減法，乗法と除法は，それぞれ逆演算である。また，加法，乗法については，結合法則，交換法則が，さらに，加法と乗法の間では，加法に対する乗法の分配法則が成り立つ。
執筆者：西村 純一

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

四則
しそく
four rules

加法，減法，乗法，除法の4つの算法をまとめて，四則あるいは四則計算という。任意の実数をa，bとするとき，a，bを，＋で結合することを加法といい，加えた結果a＋bを，aとbの和という。また，b＋x＝aを満足するxを求めることを減法 (aからbを引く) といい，このxをa-bと書いて，これをaとbの差という。a，bの乗法とは，×または・ (掛け算の意味) でa，bを結合することで，掛けた結果a×bあるいはa・b (単に abとも書く) をaとbの積という。またb×x＝a (b≠0) を満足するxを求めることを除法 (aをbで割る) といい，このxをa÷bまたはa/bと書いて，これをaとbの商という。ただし，このような掛け算の意味以外に，一般の代数系において，2元の結合をつくる算法を乗法ということもある。加法，乗法については交換法則，結合法則，分配法則，簡約法則が成り立つ。また減法と除法は，それぞれ加法と乗法の逆算である。

(1) 交換法則
　　a＋b＝b＋a
　　a×b＝b×a
(2) 結合法則
　　a＋ (b＋c) ＝ (a＋b) ＋c
　　a× (b×c) ＝ (a×b) ×c
(3) 分配法則
　　 (a＋b) ×c＝a×c＋b×c
(4) 簡約法則
　　a＋c＝a＋bならばc＝b
　　a×c＝a×bならばc＝b (a≠0)

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

四則
しそく

加法、減法、乗法、除法の四つの計算を総称していう。加法と減法、乗法と除法は、それぞれ、
　　(a＋b)－b＝a, (a－b)＋b＝a,
　　(a×b)÷b＝a, (a÷b)×b＝a
のように、互いに逆の計算になっている。また、a－b＝a＋(－b), a÷b＝a×(1/b)のように、減法は符号反対の数を加える加法、除法は逆数を乗ずる乗法に直すことができる。加法については交換法則a＋b＝b＋aおよび結合法則(a＋b)＋c＝a＋(b＋c)が、乗法については交換法則a×b＝b×aおよび結合法則(a×b)×c＝a×(b×c)が、加法と乗法については分配法則a×(b＋c)＝(a×b)＋(a×c)が成立する。さらに、加法については0、乗法については1が、特別な意味をもっている。どんな数aに対しても、a＋0＝0＋a＝a, a×1＝1×a＝aである。さらに、0については、a×0＝0×a＝0となる。

　式の四則の計算の順序は次のとおりである。

(1)加減だけ、あるいは乗除だけの式の計算は、通常の順序に従う。

(2)加減と乗除が混じっている式の計算は、乗除の計算を先に行い、その次に加減の計算を行う。

(3)括弧(かっこ)が入っている式の計算は括弧の中の計算を先にする。

［三輪辰郎］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

四則【しそく】

数に関する四つの基本演算，つまり加・減・乗・除法。四則演算は二つの有理数どうし，実数どうし，複素数どうしの間で，０による除法以外はすべて可能（一般に四則演算が成り立つ集合を体(たい)という）。なお，整数の集合，自然数の集合では，３÷５や３―５のように，演算の結果が，整数や自然数とはならず，整数の集合では除法が，自然数の集合では減法と除法が可能とは限らない。
→関連項目数（数学）

出典　株式会社平凡社