チェバの定理
ちぇばのていり
三角形ABCにおいて、頂点と異なる点をPとし、AP、BP、CPが対辺と交わるとき、その交点をそれぞれD、E、Fとすると、各辺を内分あるいは外分する三つの比の積が1になる。すなわち、
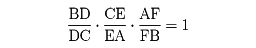
である。これをチェバの定理という。イタリアの数学者チェバGiovanni Ceva(1647?―1734)が1678年に発表した定理。この定理の逆も成り立つ。すなわち、三角形ABCの三辺BC、CA、AB上に3点D、E、Fがあり、前述の三つの比の積が1ならば、三直線AD、BE、CFは1点で交わる。ただし、3点のうち二つが辺の延長上にあるときは、頂点と結んでできる三直線が平行となることもある。
三直線が1点で交わることを示す定理を共点定理というが、チェバの定理の逆はその基本となるものである。三角形の重心、垂心、内心など、チェバの定理の逆を用いて導くことができる。
[柴田敏男]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
チェバの定理 (チェバのていり)
Ceva's theorem
イタリアのチェバG.Ceva(1647-1734)が発見した次の定理をいう。三角形ABCの辺BC,CA,AB,またはそれらの延長上にそれぞれ点D,E,Fがあり,これらは三角形ABCの頂点でないとする。このとき直線AD,BE,CFが1点で交わるか,または互いに平行になるための必要かつ十分条件は,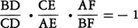 が成り立つことである。ここに上式の左辺の各分数はD,E,Fが線分BC,CA,ABの内分点であるか外分点であるかに応じて,+,または-の符号をつけて考えるものとする。
が成り立つことである。ここに上式の左辺の各分数はD,E,Fが線分BC,CA,ABの内分点であるか外分点であるかに応じて,+,または-の符号をつけて考えるものとする。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
チェバの定理
チェバのていり
Ceva's theorem
三角形に関する次の定理をいう。三角形 ABCと,その平面上の1点Pが与えられたとき,三角形の頂点A,B,Cと点Pとを結ぶ3直線が,辺 BC,CA,ABまたはその延長と交わる点をそれぞれX,Y,Zとすれば
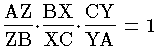 が成り立つ。この定理は,1678年に G.チェバによって発見された。この定理が成り立つときは,逆に,AX,BY,CZ は1点で交わるか,あるいは平行である。チェバの定理は次のような式でも表わすことができる。
が成り立つ。この定理は,1678年に G.チェバによって発見された。この定理が成り立つときは,逆に,AX,BY,CZ は1点で交わるか,あるいは平行である。チェバの定理は次のような式でも表わすことができる。
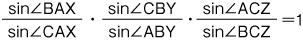 これはまた,A,B,Cに重みをおいたときに,Pを重心として,つまり重心座標で考えていることにあたる。
これはまた,A,B,Cに重みをおいたときに,Pを重心として,つまり重心座標で考えていることにあたる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
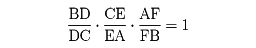

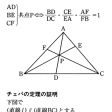

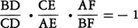 が成り立つことである。ここに上式の
が成り立つことである。ここに上式の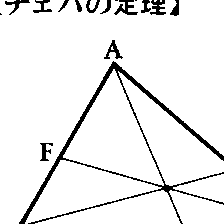
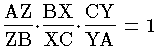 が成り立つ。この定理は,1678年に G.チェバによって発見された。この定理が成り立つときは,逆に,AX,BY,CZ は1点で交わるか,あるいは平行である。チェバの定理は次のような式でも表わすことができる。
が成り立つ。この定理は,1678年に G.チェバによって発見された。この定理が成り立つときは,逆に,AX,BY,CZ は1点で交わるか,あるいは平行である。チェバの定理は次のような式でも表わすことができる。 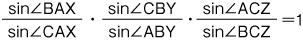 これはまた,A,B,Cに
これはまた,A,B,Cに