関連語
精選版 日本国語大辞典 「デルタ関数」の意味・読み・例文・類語
デルタ‐かんすう‥クヮンスウ【デルタ関数】
日本大百科全書(ニッポニカ) 「デルタ関数」の意味・わかりやすい解説
デルタ関数
でるたかんすう
デルタ関数はディラックが1925年ころ量子力学の理論体系を整備するために導入したもので、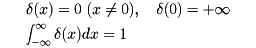
という性質をもつものとして定義された。したがって、これは普通にいう関数ではないが、ディラックは物理学的な直観から、実軸上の連続関数 (x)に対し、
(x)に対し、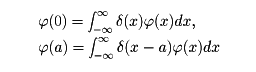
という公式や、また、デルタ関数の微分を考え、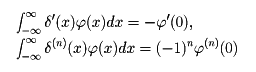
などの公式を導き、積分因子としては積分の値が決まるものとし、しかも、いろいろな物理現象の計算に有効に使った。このような形式的な取扱いに数学的に厳密な証明を与える試みはいくつかあったが、1950年ころL・シュワルツが超関数の理論をつくり、これを完全に解決した。無限回連続微分可能な関数で、|x|が大きいところでは恒等的に0になる関数の集合を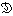 で表し、
で表し、 (x)∈
(x)∈ に対し、線形汎(はん)関数δをδ(
に対し、線形汎(はん)関数δをδ( )=
)= (0)で表すと、δは超関数になる。これをディラックの伝統に従って
(0)で表すと、δは超関数になる。これをディラックの伝統に従って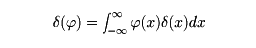
と書き、超関数の微分法に従って微分すると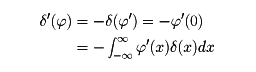
など、前に書いた微分の公式が得られる。
関数 (x)のフーリエ変換を
(x)のフーリエ変換を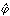 (ξ)で表す。超関数のフーリエ変換の定義に従って、デルタ関数のフーリエ変換を計算すると、
(ξ)で表す。超関数のフーリエ変換の定義に従って、デルタ関数のフーリエ変換を計算すると、
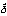 =1,
=1,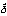 ′=iξ,……,
′=iξ,……,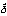 (m)=(iξ)m
(m)=(iξ)m
となる。この性質は、応用において重要である。
[洲之内治男]
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

