翻訳|distribution
改訂新版 世界大百科事典 「超関数」の意味・わかりやすい解説
超関数 (ちょうかんすう)
distribution
Ωをm次元ユークリッド空間の中の領域とし,m個の負でない整数の組p=(p1,……,pm)に対して|p|=p1+……+pm,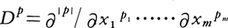 とする。KをΩの中の任意のコンパクト集合とし,Ω上で無限回微分可能な複素数値関数で,あるKの外では0になるもの全体を
とする。KをΩの中の任意のコンパクト集合とし,Ω上で無限回微分可能な複素数値関数で,あるKの外では0になるもの全体を kと書き,
kと書き,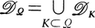 とする。関数列{φn}⊂
とする。関数列{φn}⊂
 が0に近づくとは,{φn}があるKに対する
が0に近づくとは,{φn}があるKに対する kに含まれ,任意の偏微分演算Dpに対して{Dpφn}がΩ上で一様に0に収束すると定義し,そのときφn→0と書く。関数空間
kに含まれ,任意の偏微分演算Dpに対して{Dpφn}がΩ上で一様に0に収束すると定義し,そのときφn→0と書く。関数空間
 上の複素数値線形汎関数Tが連続性,
上の複素数値線形汎関数Tが連続性,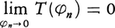 を満たすとき,TをΩ上の超関数という。
を満たすとき,TをΩ上の超関数という。
1945年,シュワルツL.Schwartzは〈部分積分を通しての関数概念の拡張〉であるところの超関数の理論を創始した。この理論によって,その後,フーリエ解析や偏微分方程式の理論は著しい発展を見せた。
超関数の例
(1)fをΩ上の連続関数として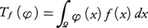 と定義したもの,(2)μをΩ上の測度として
と定義したもの,(2)μをΩ上の測度として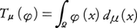 と定義したもの,(3)1点x°∈Ωを固定して
と定義したもの,(3)1点x°∈Ωを固定して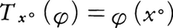 と定義したものはいずれも超関数である。とくに(3)は点x°におけるディラックのδ関数と呼ばれる。
と定義したものはいずれも超関数である。とくに(3)は点x°におけるディラックのδ関数と呼ばれる。
上の(1)において,もしも∂f(x)/∂x1が存在して連続ならば,部分積分からわかるように となる。一般に,任意の超関数Tと偏微分演算Dpに対して
となる。一般に,任意の超関数Tと偏微分演算Dpに対して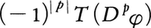 をφ∈
をφ∈
 の線形汎関数と考えると,超関数の条件を満たすので,
の線形汎関数と考えると,超関数の条件を満たすので,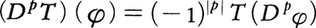 によって超関数Tの偏導超関数DpTを定義する。これにより,任意の超関数は無限回偏微分可能である。例えばTを前述の(3)におけるTx°とすると
によって超関数Tの偏導超関数DpTを定義する。これにより,任意の超関数は無限回偏微分可能である。例えばTを前述の(3)におけるTx°とすると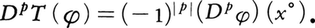
超関数の算法
超関数T,Sの和T+SおよびTの定数α倍は,それぞれ,任意のφ∈
 に対して,(T+S)(φ)=T(φ)+S(φ)および(αT)(φ)=α・T(φ)によって定義する。また,Ωで無限回微分可能な関数ψと超関数Tとの積は(ψT)(φ)=T(ψφ)(φ∈
に対して,(T+S)(φ)=T(φ)+S(φ)および(αT)(φ)=α・T(φ)によって定義する。また,Ωで無限回微分可能な関数ψと超関数Tとの積は(ψT)(φ)=T(ψφ)(φ∈
 )により定義する。したがってとくに,Ωで連続な関数fに対してはψTf=Tψfとなる。以上のことを使うと無限回微分可能な関数ap(x)を係数とする偏微分作用素,
)により定義する。したがってとくに,Ωで連続な関数fに対してはψTf=Tψfとなる。以上のことを使うと無限回微分可能な関数ap(x)を係数とする偏微分作用素,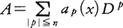 が定義される。このAに対して,
が定義される。このAに対して,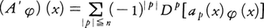 で定義される偏微分作用素A′をAの随伴偏微分作用素という。このとき任意の超関数Tに対して(AT)(φ)=T(A′φ)なる関係がある。これは,Tが無限回微分可能な関数fによってT=Tf(前述の例(1))と表されている場合は,ふつうの部分積分によって得られる式,
で定義される偏微分作用素A′をAの随伴偏微分作用素という。このとき任意の超関数Tに対して(AT)(φ)=T(A′φ)なる関係がある。これは,Tが無限回微分可能な関数fによってT=Tf(前述の例(1))と表されている場合は,ふつうの部分積分によって得られる式,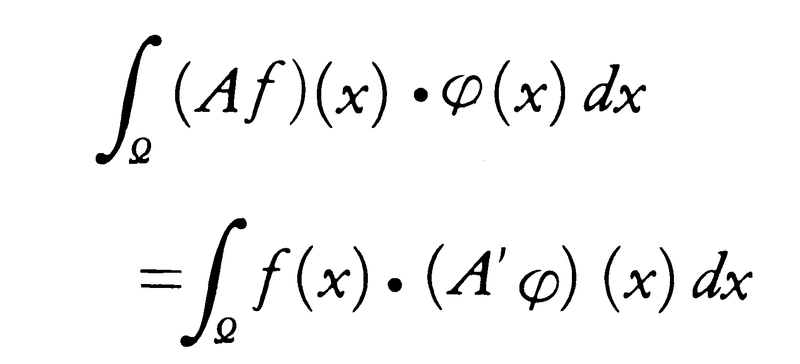
にほかならない。
偏微分方程式への応用例
もっとも著しい結果は,楕円型偏微分方程式に関するものであろう。2階偏微分作用素,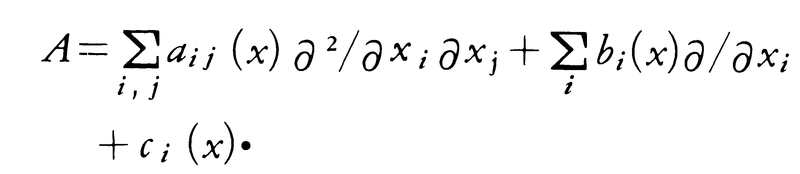
は,各点x∈Ωにおいて二次形式,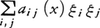 が正の定値(すなわち,
が正の定値(すなわち,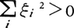 である限り
である限り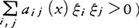 )であるとき,Aは楕円型であるという。例えばラプラシアンΔ=∂2/∂x12+……+∂2/∂xm2は楕円型偏微分作用素である。上記の楕円型偏微分作用素Aにおいて,各係数aij(x),bi(x),c(x)が無限回微分可能であり,また,f(x)を無限回微分可能な既知関数とするとき,超関数の理論によれば偏微分方程式AT=fを満たす超関数Tがあれば(すなわち, 任意のφ∈
)であるとき,Aは楕円型であるという。例えばラプラシアンΔ=∂2/∂x12+……+∂2/∂xm2は楕円型偏微分作用素である。上記の楕円型偏微分作用素Aにおいて,各係数aij(x),bi(x),c(x)が無限回微分可能であり,また,f(x)を無限回微分可能な既知関数とするとき,超関数の理論によれば偏微分方程式AT=fを満たす超関数Tがあれば(すなわち, 任意のφ∈
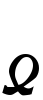 に対して
に対して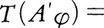
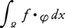 が成立すれば),無限回微分可能な関数uで偏微分方程式Au=fを満たすものが存在してT=Tuとなる(この事実はワイル=シュワルツの補題と呼ばれる)。簡略ないい方をすれば,楕円型偏微分方程式AT=fの超関数解Tは,実はふつうの意味のAu=fの解uになるのである。超関数は関数空間
が成立すれば),無限回微分可能な関数uで偏微分方程式Au=fを満たすものが存在してT=Tuとなる(この事実はワイル=シュワルツの補題と呼ばれる)。簡略ないい方をすれば,楕円型偏微分方程式AT=fの超関数解Tは,実はふつうの意味のAu=fの解uになるのである。超関数は関数空間
 の上の連続線形汎関数として定義されているので,現代の関数解析学の手法を用いることにより,超関数解を求めることは,最初からふつうの関数の解を求めるよりも容易なことが多いが,その超関数解がワイル=シュワルツの補題によりふつうの解になっているのである。以上のことは放物型偏微分方程式についても成立する。すなわち,実数tの区間Iと領域Ω⊂Rmとの直積において∂T/∂t=AT+f(A,fは上に述べたとおり)を満たす超関数Tがあれば,I×Ωにおける偏微分方程式∂u/∂t=Au+fのふつうの解uが存在してT=Tuとなる。これに対し,双曲型偏微分方程式についてはワイル=シュワルツの補題は成立しない。例えば,f(x),g(y)をそれぞれ実数x,yのみの関数とするとき,二次元領域における方程式∂2T/∂x∂y=0は超関数解
の上の連続線形汎関数として定義されているので,現代の関数解析学の手法を用いることにより,超関数解を求めることは,最初からふつうの関数の解を求めるよりも容易なことが多いが,その超関数解がワイル=シュワルツの補題によりふつうの解になっているのである。以上のことは放物型偏微分方程式についても成立する。すなわち,実数tの区間Iと領域Ω⊂Rmとの直積において∂T/∂t=AT+f(A,fは上に述べたとおり)を満たす超関数Tがあれば,I×Ωにおける偏微分方程式∂u/∂t=Au+fのふつうの解uが存在してT=Tuとなる。これに対し,双曲型偏微分方程式についてはワイル=シュワルツの補題は成立しない。例えば,f(x),g(y)をそれぞれ実数x,yのみの関数とするとき,二次元領域における方程式∂2T/∂x∂y=0は超関数解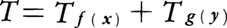 をもつが,ここでf,gは不連続関数でもよいのである。
をもつが,ここでf,gは不連続関数でもよいのである。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「超関数」の意味・わかりやすい解説
超関数
ちょうかんすう
ディラックのデルタ関数は物理学では有効に用いられてきたが、数学的には関数の定義に当てはまらない。そこでシュワルツはこれらを含むように、しかも微分演算やフーリエ解析が自由にできるように関数概念を拡張した。シュワルツはそれをdistributionsと名づけたが、日本では超関数とよんでいる。応用上は多変数の関数を考えることが多いが、一変数の場合にその考え方を紹介しておこう。実変数xの、無限回連続微分可能で、|x|が大きいとき恒等的に0になる関数の集合を で表す。いま、f(x)を連続関数とすると、
で表す。いま、f(x)を連続関数とすると、 (x)∈
(x)∈ に対し、
に対し、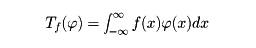
は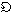 上の線形汎関数(はんかんすう)になり、次の意味で連続になる。任意の有限区間Iに対し、Iの外で0になる
上の線形汎関数(はんかんすう)になり、次の意味で連続になる。任意の有限区間Iに対し、Iの外で0になる (x)∈
(x)∈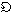 に対し
に対し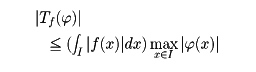
一般に、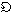 上の線形汎関数T(
上の線形汎関数T( )で、任意の有限区間Iを与えると、定数M、自然数pが決まり、Iの外で0となる任意の関数
)で、任意の有限区間Iを与えると、定数M、自然数pが決まり、Iの外で0となる任意の関数 (x)∈
(x)∈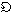 に対し、
に対し、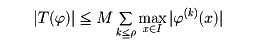
となるとき、Tを超関数という。たとえば、
δ( )=
)= (0)
(0)
として定義されるδも超関数(ディラックのデルタ関数)である。超関数S、Tが等しい(S=T)とは、任意の (x)∈
(x)∈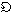 に対し、S(
に対し、S( )=T(
)=T( )となることとする。超関数Tの微分は、
)となることとする。超関数Tの微分は、 (x)∈
(x)∈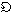 ならば、その導関数
ならば、その導関数 ′(x)∈
′(x)∈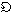 を用い、-T(
を用い、-T( ′)を
′)を の汎関数と考えると、超関数T′が、
の汎関数と考えると、超関数T′が、
T′( )=-T(
)=-T( ′)
′)
として決まる。このT′をTの(超関数としての)導関数という。これが自然な定義であることは、f(x)が微分可能ならば、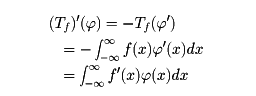
が部分積分より、ゆえに(Tf)′=Tf'となることよりわかる。
ヘビサイド関数
H(x)=0(x<0),
H(x)=1(x>0)
を超関数と考えて微分すると、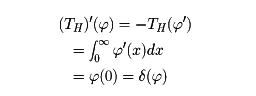
より、(TH)′=δで、これも応用上重要な関係である。超関数Tに微分が定義できるから、超関数の意味で微分方程式を考えることができる。とくに、
P(D)T=a0(x)T(n)+a1(x)T(n-1)+
……+an(x)T=δ
を満足する超関数Tを基本解という。基本解が求まると、任意の右辺に対する解が求まるので、微分方程式では基本解を求めることが問題になる。
[洲之内治男]
超関数のフーリエ変換
フーリエ変換の定義できる自然な関数として、急減少関数(無限回連続微分可能、任意の自然数m、nに対し、|x|→∞のとき、|xm (n)(x)|→0となるもの)がある。その集合を
(n)(x)|→0となるもの)がある。その集合を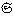 で表すと、
で表すと、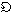 ⊂
⊂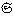 となる。
となる。 (x)∈
(x)∈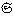 のフーリエ変換を
のフーリエ変換を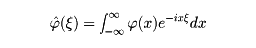
で定義する。すると、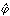 (ξ)∈
(ξ)∈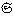 となり、逆変換として
となり、逆変換として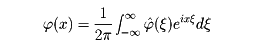
が成り立つ。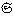 上の連続な線形汎関数として決まる超関数Tを緩やかな超関数という。これにも微分が前と同様に定義できるが、さらに、フーリエ変換を、
上の連続な線形汎関数として決まる超関数Tを緩やかな超関数という。これにも微分が前と同様に定義できるが、さらに、フーリエ変換を、 (x)∈
(x)∈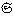 を用いて、
を用いて、
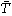 (
( )=T(
)=T(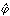 )
)
として決まる緩やかな超関数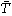 で定義する。
で定義する。
デルタ関数δのフーリエ変換は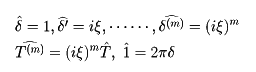
などがいえる。
[洲之内治男]
偏微分熱方程式への応用例
無限に長い針金の熱伝導は、時刻t、場所xにおける温度をu(t,x)とすると、熱方程式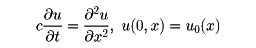
で与えられる。u(t,x)を、tをパラメーター、xの関数として(超関数として)フーリエ変換をとると、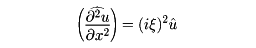
となるから、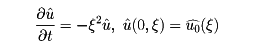
これはξをパラメーターと考えると、tの常微分方程式、よって解は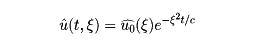
となる。よって、これのフーリエ逆変換が求まれば、それが求める解である。
[洲之内治男]
ブリタニカ国際大百科事典 小項目事典 「超関数」の意味・わかりやすい解説
超関数
ちょうかんすう
distribution
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の超関数の言及
【ゲルファント】より
…モスクワ大学に学び,1943年からモスクワ大学教授。ノルム環の理論の創始者であり,また超関数の理論の創始者の一人でもある。1940年に発表した連続群の表現論に関する研究は高く評価されている。…
※「超関数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

