改訂新版 世界大百科事典 「フレドホルム」の意味・わかりやすい解説
フレドホルム
Erik Ivar Fredholm
生没年:1866-1927
スウェーデンの数学者。ストックホルムに生まれストックホルムに没する。1886年にウプサラ大学に入学,ここで学位をとり,ストックホルム大学でミッターク・レフラーG.M.Mittag-Lefflerに師事し,1906年に力学と数理物理担当の教授となった。彼の最大の業績は1900年に得られた積分方程式,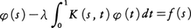 に関するものである。すなわち,核と呼ばれる連続関数K(s,t)とパラメーターλの値λ0が与えられたときには,〈すべての連続関数fに対してただ一つの連続関数解φ(s)が存在するか,または,
に関するものである。すなわち,核と呼ばれる連続関数K(s,t)とパラメーターλの値λ0が与えられたときには,〈すべての連続関数fに対してただ一つの連続関数解φ(s)が存在するか,または,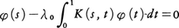 が0でない連続解φ(s)を有限個もつかのいずれかが成り立つ〉という定理であり,〈フレドホルムのオールタナティブ〉とも呼ばれる。上の積分方程式は,〈特殊の核K(x,y)と特殊のλの値の場合〉にはC.ノイマンがポテンシャル論に関連して取り扱った(1884)ものであった。フレドホルムの研究は,彼の友人ホルムグレンErik Holmgrenによってゲッティンゲン大学のD.ヒルベルトに伝えられ(1901),ヒルベルトによって今日〈ヒルベルト空間論〉といわれている〈スペクトル理論〉に発展した。
が0でない連続解φ(s)を有限個もつかのいずれかが成り立つ〉という定理であり,〈フレドホルムのオールタナティブ〉とも呼ばれる。上の積分方程式は,〈特殊の核K(x,y)と特殊のλの値の場合〉にはC.ノイマンがポテンシャル論に関連して取り扱った(1884)ものであった。フレドホルムの研究は,彼の友人ホルムグレンErik Holmgrenによってゲッティンゲン大学のD.ヒルベルトに伝えられ(1901),ヒルベルトによって今日〈ヒルベルト空間論〉といわれている〈スペクトル理論〉に発展した。
執筆者:吉田 耕作
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


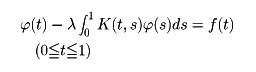
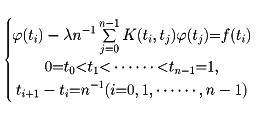
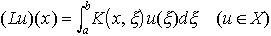 と定義する。Lをフレドホルム型の積分作用素,K(x,ξ)をその核と呼ぶ。このとき,
と定義する。Lをフレドホルム型の積分作用素,K(x,ξ)をその核と呼ぶ。このとき,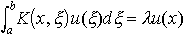 を満たす恒等式に0でない関数u∈Xが存在すれば,λはLの固有値である。…
を満たす恒等式に0でない関数u∈Xが存在すれば,λはLの固有値である。…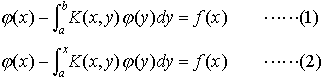 はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…
はそれぞれフレドホルム型積分方程式,ボルテラ型積分方程式と呼ばれ,K(x,y)をこれらの方程式の核という。…