偏微分法（読み）へんびぶんほう

日本大百科全書(ニッポニカ)

偏微分法
へんびぶんほう

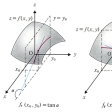
多変数の関数において、ある変数に注目し、残りの変数を固定しておいて、注目する変数で微分することを、この変数について偏微分するという。このような微分演算と、その利用についての理論の体系が偏微分法である。以下では二変数の場合について説明する。関数のうち多変数の関数がある。たとえば、直角三角形で、斜辺zは、直角を挟む二辺x、yによって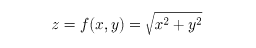

と表される。いまここで、x、yのうち、たとえばyは変化しないものとすれば、zはxだけの関数とみることができ、変数xについて微分することができる。これがxについての偏微分である。x=x₀,y=y₀の近傍で定義された関数f(x,y)は、yを一定値y₀に固定して得られるxの関数f(x,y₀)がx=x₀において微分可能であるとき、(x₀,y₀)においてxに関して偏微分可能であるといい、この微分係数の値を、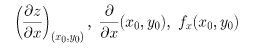

などで表す。すなわち、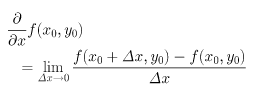

これをf(x,y)の(x₀,y₀)におけるxに関する偏微分係数という。同様に、yに関する偏微分係数も定められる（図）。

　領域Gで定義されたf(x,y)に対し、その領域の各点でf(x,y)がxに関して偏微分可能ならば、各点に、その点での偏微分係数の値を対応させた関数が得られる。これをf(x,y)のxに関する偏導関数といい、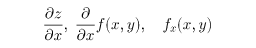

などで表す。同様にyに関する偏導関数も定義される。たとえばf(x,y)=x²+y²のときf_x(x,y)=2x,f_y(x,y)=2yである。偏微分の方法は、一変数に関する通常の微分の方法の適用の繰り返しだが、とくに合成関数の微分法については表に示す連鎖法則がある。f(x,y)の偏導関数が、さらに偏微分可能のとき、偏導関数の偏導関数が考えられる。たとえば、f_xyy(x,y)は、f(x,y)をまずxで偏微分し、次にyで2回偏微分したものを表すものとする。このような偏導関数を高階偏導関数という。一階偏導関数はf_x,f_yの2個、二階偏導関数はf_xx,f_xy,f_yx,f_yyの2²=4個、……、k階偏導関数は2^k個ある。これらがすべて存在して連続であるとき、f(x,y)はC^k級関数であるという。C^k級関数では、偏導関数は、偏微分の順序には関係しない。たとえば、f_xy(x,y)=f_yx(x,y)で、したがって二階偏導関数のうち異なるものは3個、三階偏導関数では4個、……、k階偏導関数ではk+1個ある。

［竹之内脩］

偏微分法説明図〔図〕

偏微分法（連鎖法則）〔表〕

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の偏微分法の言及

【微分】より

…こうすると，　dy＝f′(a)dxとなり，微分係数の記号dy/dx＝f′(a)と対応する。
【偏微分法】
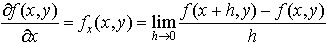　二つ以上の変数x,y，……の関数f(x,y，……)があるとき，これを一つの変数，例えばxだけに注目して，他の変数は固定して定数と考え，xの関数と考えて微分することを，関数fをxについて偏微分するといい，それによって得られる微分係数を，変数xに関するfの偏微分係数と呼んで∂f/∂x，またはf_xと書く。簡単のために2変数の関数f(x,y)について書くと，によってfのxに関する偏微分係数が定義される。…

※「偏微分法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」