冪級数（読み）ベキキュウスウ

デジタル大辞泉

べき‐きゅうすう〔‐キフスウ〕【^×冪級数】

a_n（n＝0,1,2,…）はxを含まない数として、a₀＋a₁x＋a₂x²＋…a_nxⁿ…の形の級数。整級数。

出典　小学館

改訂新版　世界大百科事典

冪級数 (べききゅうすう)
power series

べきとは累乗のことで，c，a₀，a₁，……を複素定数，zを複素変数とした級数，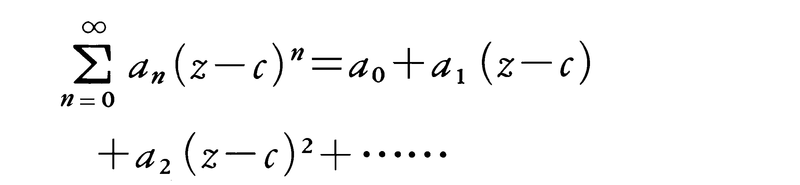

のことを，cを中心とする（1変数）べき級数という。また，整級数ともいう。

　微積分学ではc，a_n，zが実数に限られたものを扱うが，そのときも，zは複素数に拡張して考えたほうが利点が多い。

　与えられたべき級数において，それが収束するようなzに対する｜z－c｜の上限ρを収束半径といい，円｜z－c｜＝ρを収束円という。次の公式（コーシー=アダマールの公式Cauchy-Hadamard's formula）がある。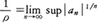

　0＜ρ≦∞のとき，べき級数は収束円内で絶対収束し，また任意のρ′＜ρに対して，｜z－c｜≦ρ′で一様収束する。和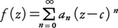は収束円内で正則な関数であり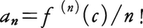，が成り立つ。逆に，正則関数は定義域に含まれる円板内において，その中心を中心とするべき級数に展開できる。したがって，正則関数の局所的な議論はべき級数の議論と本質的には相違ない。しかも解析接続によって大域的な議論を行うこともできるのであって，この理論はK.ワイヤーシュトラスによって創始された。

　べき級数は2変数以上の場合にも考えられる。2変数zとwのときは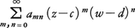，の形をしている。
執筆者：及川 廣太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」