日本大百科全書(ニッポニカ) 「整級数」の意味・わかりやすい解説
整級数
せいきゅうすう
aを複素数、{cn}を複素数列とするとき、zを変数とする級数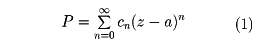
を整級数、またはべき級数という。たとえば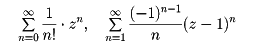
などがそうである。整級数(1)に対し、0≦R≦∞なるRが一つ定まって、|z-a|<Rならば(1)は収束し、|z-a|>Rならば(1)は発散する。このRを整級数(1)の収束半径という。またこのとき、円|z-a|=Rを収束円という。前記の例では収束半径はそれぞれ∞と1である。収束半径の値はコーシー‐アダマールの公式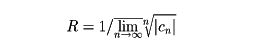
で与えられる。R>0のとき、収束円の内部Dの点zに対し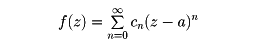
と置いてD上の関数を定めると、f(z)はD上正則関数になり、導関数は項別微分により得られる。よってf(z)は何回でも微分可能で、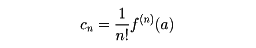
が成り立つ。逆にある領域で正則な関数はその領域の各点の近傍で整級数に展開される。一般に収束半径が0より大きい整級数を関数要素とよび、一つの関数要素から解析接続により得られる関数要素の全体が解析関数である。
整級数はその収束円上のzに対しては収束することも発散することもある。
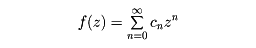
の収束半径が1で、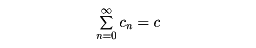
が収束するならば、xを実数として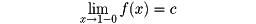
である(アーベルの連続性定理)。しかし、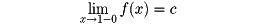
が収束しても、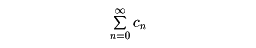
は収束するとは限らない。
整級数は多変数の場合にも定義される。たとえば、a,b,cn,mを複素数とし、z、wを変数として級数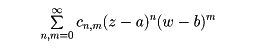
は二変数整級数である。
[小林良和]
ブリタニカ国際大百科事典 小項目事典 「整級数」の意味・わかりやすい解説
整級数
せいきゅうすう
「べき級数」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の整級数の言及
【べき級数(冪級数)】より
…べきとは累乗のことで,c,a0,a1,……を複素定数,zを複素変数とした級数,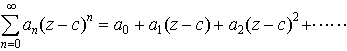 のことを,cを中心とする(1変数)べき級数という。また,整級数ともいう。 微積分学ではc,an,zが実数に限られたものを扱うが,そのときも,zは複素数に拡張して考えたほうが利点が多い。…
のことを,cを中心とする(1変数)べき級数という。また,整級数ともいう。 微積分学ではc,an,zが実数に限られたものを扱うが,そのときも,zは複素数に拡張して考えたほうが利点が多い。…
※「整級数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

