固有関数（読み）コユウカンスウ

化学辞典 第2版

固有関数
コユウカンスウ
characteristic function, eigen function

その解に対してある条件が付されている微分方程式の固有値問題において，ある固有値に対応した解を固有関数という．一例として，質量mの粒子が振動数νで一次元振動を行い，その変位がx，全エネルギーがEの場合を述べる．

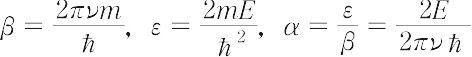
としてξ 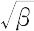＝ xの変数変換をすれば，波動関数(状態関数)φ(x)は，

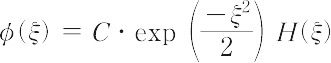
と書けて，H(ξ)は微分方程式，

H″(ξ) － 2ξH′(ξ) ＋ 2λH(ξ) ＝ 0

を満たさなければならない．ただし，λ ＝ 0，1，2でα ＝ 2λ ＋ 1が固有値条件である．このλのおのおのの値に対応する解H_λ(ξ)はエルミートの多項式といわれるもので，

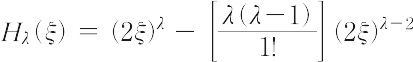
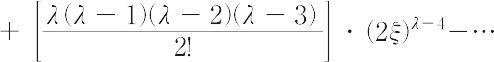
と書け，最高次数はλ，最低次数はλの偶奇に応じて0次定数か一次であって，自乗積分可能の条件が満たされる．全体の波動関数は，

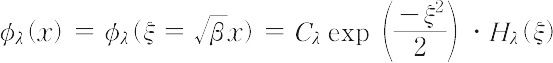
であり，これが固有値λに対応する固有関数である．定数 C_λ は，自乗積分が，

∫_－∞^∞φ (x)²dx ＝ 1

であるようにλに対して定めるもので，

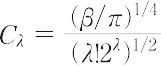
となる．これを規格化の定数という．量子力学特有の結論として，古典論では粒子が静止している状態に対応するλ ＝ 0の状態でも，

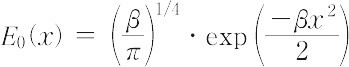
であって，ある広がりをもっている．これは不確定性原理を反映したものである．また，H_λ(ξ)が最高次数項 (2ξ)^λ から二次ずつ下がった項の和であるため，λの偶奇に対応して φ_λ(－x) ＝ φ_λ(x)または φ_λ(－x) ＝ － φ_λ(x)の関係がある．これは調和振動子の量子状態は，λ ＝ 偶数のときはパリティ(偶奇性)が偶であり，λ ＝ 奇数のときはパリティが奇であることを示している．

出典　森北出版「化学辞典（第2版）」

世界大百科事典（旧版）内の固有関数の言及

【固有値】より

…X,Yは線形空間でYはXを部分空間として含むものとし，LをXからYへの線形作用素とするとき，Lu＝λu(λは定数)となるようなu∈Xがu＝0以外に存在するとき，λをLの固有値，uをそれに対応する固有ベクトル(Xが関数空間である場合には固有関数)といい，固有値および固有ベクトルを求める問題を固有値問題という。いくつかの具体例をあげよう。…

【積分方程式】より

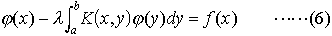…　(1)の核に助変数λを含ませた方程式，を考えることが多い。この右辺を0で置き換えた方程式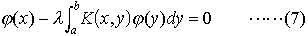，については，φ₀(x)≡0なるφ₀は一つの解であるが，(7)がこのφ₀以外の解φをもつようなλを固有値といい，そのときの解φを固有値λに属する固有関数という。　K(x,y)が実数値で，かつK(x,y)＝K(y,x)を満たすとき，これを対称核という。…

【量子力学】より

…こうして量子力学は光の放出という瞬間的な遷移(時間的に不連続な過程)を確率を介して波動関数α_nψ_n＋α_n′ψ_n′の時間空間的に連続な変化に直して記述している。
［観測量と固有関数］
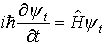　シュレーディンガー方程式は一般に，という形をしている(i²＝－1，ħ＝h/2π)。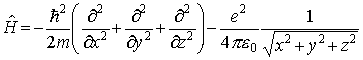は，たとえば水素原子の電子の場合でいえば，電子の質量をm，電荷を－e，真空の誘電率をε₀として，の形であり，電子の位置座標に相当するr＝(x,y,z)の関数ψ_t＝ψ_t(x,y,z)に作用してこれを別の関数に変える働きをもつ。…

※「固有関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」