調和振動子（読み）チョウワシンドウシ（英語表記）harmonic oscillator

デジタル大辞泉

ちょうわ‐しんどうし〔テウワ‐〕【調和振動子】

単振動を行う系。ある質点が原点からの距離に比例する引力を受けるときの運動に等しい。

出典　小学館

改訂新版　世界大百科事典

調和振動子 (ちょうわしんどうし)
harmonic oscillator

振子のように振動する物体のうち，とくに平衡の位置Oへの引戻しの力が，Oからのずれ（変位）に比例する種類のもの。たいていの振動は振幅が十分に小さいとき調和振動子で近似することができる。Oからの変位をxとすれば，引戻しの力は，xが正のとき負の向き，xが負のとき正の向きをむくので，－kxと書ける。kは正の比例定数で，しばしばばね定数と呼ばれる。振動子の質量をm，時刻をtとすれば，その運動x＝x（t）を決める運動方程式はmd²x/dt²＝－kxとなる。時刻t＝0において位置がx₀，速度がv₀だったとすると，運動方程式の解はx＝x₀cosωt＋（v₀/ω）sinωtとなる。 ただし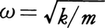は角振動数と呼ばれ，振動の周期TとはT＝2π/ω，振動数νとはω＝2πνの関係にある。

　量子力学の世界では，調和振動子はE_n＝（n＋1/2）ħω（n＝0，1，……）という離散的なエネルギーしかとらない（ħはプランク定数を2πで割ったもの）。その最低の値が0でないのは不確定性原理によるためで，対応する運動を零点振動と呼ぶ。結晶格子の振動や電磁場など素粒子の場は，量子力学的には第0近似で調和振動子の集りとして記述される。そのとき電磁場の場合ならnはフォトン（光子）の数を表す。
執筆者：江沢 洋

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

調和振動子
ちょうわしんどうし

単振動は調和振動ともよばれる。調和振動をする質点や、その他の力学系は調和振動子とよばれる。古典力学では、調和振動をする質点の位置座標をx、運動量をpとすると、そのエネルギーEは、運動エネルギーと位置のエネルギーの和として
　　E=p²/(2m)+(1/2)kx²
である。ここにmは質点の質量、kは復元力(-kx)の比例定数である。この質点は振動数ν=(k/m)^1/2/2πの振動をする。量子力学では、調和振動子のエネルギーは連続的な値をとることができず、離散的な値
　　E=(n+1/2)hν　(n=0,1,2,……)
をとる。hはプランク定数である。したがって、エネルギー最低の状態（基底状態）では、E=hν/2である。このエネルギーを零点エネルギーという。またhνをエネルギー量子という。固体の熱振動、有限の体積（空洞）の中に閉じ込められた電磁波の定常波は、いずれも基準振動の重ね合わせとして表され、各基準振動は一つの調和振動子とみなされる。したがって、そのエネルギーも離散的な値をとる。エネルギー量子は、固体の熱振動ではフォノン、電磁波の定常波ではフォトンとよばれる。正整数nは、フォノンまたはフォトンの個数と解される。

　単振動の振幅が大きい場合には、振動子の位置エネルギーには、変位xの三乗以上の項が加わる。この場合の振動子は非調和振動子とよばれる。

［飼沼芳郎］

出典　小学館　日本大百科全書(ニッポニカ)

化学辞典 第2版

調和振動子
チョウワシンドウシ
harmonic oscillator

一般には，系のポテンシャルがある基準点ないし平衡位置からの変位の2乗に比例して増大する力学系をいう．たとえば，フックの法則に従うバネで壁につながれた質点は，もっとも簡単な調和振動子を形づくる．物体の弾性振動や電気振動などに現れる基本的な振動体モデルである．分子を構成する原子がその平衡配置を中心として振動する分子振動において，その振幅があまり大きくならないかぎり，調和振動子の和とみなすとよい近似になることが知られている．

出典　森北出版「化学辞典（第2版）」

ブリタニカ国際大百科事典 小項目事典

調和振動子
ちょうわしんどうし

「振動子」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の調和振動子の言及

【振動】より

…方程式(2)は，おもりに対してつねにつり合いの位置へ引き戻す向きに力が働き，その大きさはつり合いの位置からの変位ξに比例して大きくなることを示している。このような性質の力を受けて起こる振動を単振動，または調和振動といい，調和振動をしている物体を調和振動子と呼ぶ。　さて方程式(2)に従う運動は時間tの関数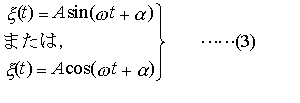，によって表される。…

【非線形力学】より

…また以下では，例えばẋとかけば，これは時間微分dx/dtを表すことにする(＝d²x/dt²)。
［調和振動子］
　ẋ＝p，ṗ＝－ω²x質点の静止点からの変位x(t)がつねにxに比例する力によって引き戻される場合，質点は理想的な振動，すなわちAcosωt＋Bsinωtのように表される運動を行う。これはニュートンの運動方程式がxに関し線形で，調和振動と呼ばれるものである。…

※「調和振動子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」