改訂新版 世界大百科事典 「密度関数」の意味・わかりやすい解説
密度関数 (みつどかんすう)
density function
確率密度関数の意味に用いられることが多い。例えば,正規分布の密度関数は,
であって,区間[a,b]にある確率は,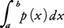 であり,また分布関数は,
であり,また分布関数は,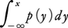 で与えられる。一般に,分布関数F(x)は,
で与えられる。一般に,分布関数F(x)は,
F(x)=a1F1(x)+a2F2(x)+a3F3(x) (a1,a2,a3≧0,a1+a2+a3=1)
の形に表される。ここにF1(x)は離散型分布,F2(x)は特異な連続分布,F3(x)がいま問題にする絶対連続分布に対応する分布関数である。F3(x)に対しては,可測関数p(x)≧0が定まって,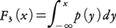 となる。このp(x)が密度関数,あるいは分布密度と呼ばれる。二項分布やポアソン分布は離散型で上のF1(x)にあたる分布関数をもつが,正規分布はF3(x)だけの分布である。ほかによく知られている密度関数は,指数分布,一様(長方形)分布,コーシー分布などに対するものがあり,それぞれ,λ>0として,
となる。このp(x)が密度関数,あるいは分布密度と呼ばれる。二項分布やポアソン分布は離散型で上のF1(x)にあたる分布関数をもつが,正規分布はF3(x)だけの分布である。ほかによく知られている密度関数は,指数分布,一様(長方形)分布,コーシー分布などに対するものがあり,それぞれ,λ>0として,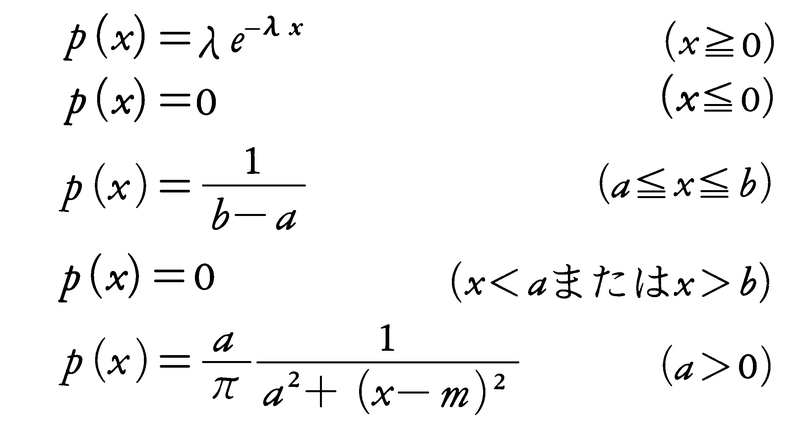
である。多次元空間上の確率分布についても同様に密度関数が考えられる。例えば二次元ガウス分布は次のような密度関数をもつ。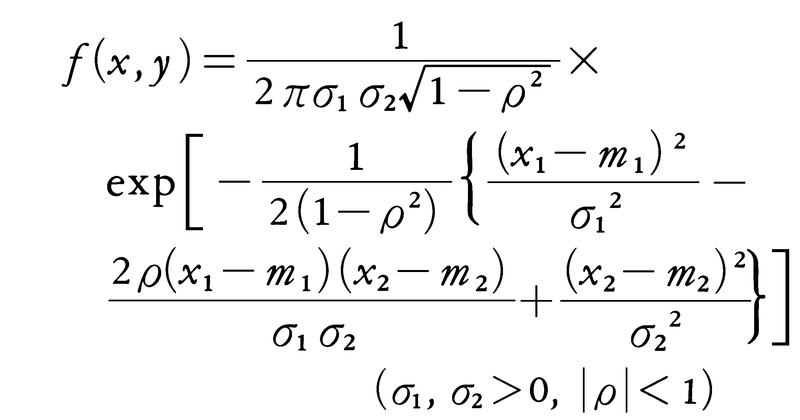
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


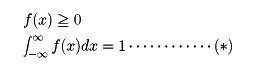
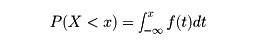
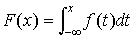 と表されるとき,Xは連続形であるといい,f(x)を密度関数と呼ぶ。 離散形の場合に戻って分布の例をあげよう。…
と表されるとき,Xは連続形であるといい,f(x)を密度関数と呼ぶ。 離散形の場合に戻って分布の例をあげよう。…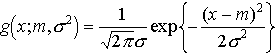 実際,前述の解熱剤の例でいえば,その効果は下がった体温の量で表され,基本的にはある定まった値(平均値m)であるが,患者の体質や病状などに個人差があって,mからの偶然誤差が生ずる。…
実際,前述の解熱剤の例でいえば,その効果は下がった体温の量で表され,基本的にはある定まった値(平均値m)であるが,患者の体質や病状などに個人差があって,mからの偶然誤差が生ずる。…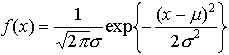 で与えられる。これはμを中心とし,富士山を投影したような形をしている。…
で与えられる。これはμを中心とし,富士山を投影したような形をしている。…