確率分布（読み）カクリツブンプ（その他表記）probability distribution

デジタル大辞泉

かくりつ‐ぶんぷ【確率分布】

確率変数のとる値に対し、その値をとる確率の分布状態。

出典　小学館

精選版 日本国語大辞典

かくりつ‐ぶんぷ【確率分布】

1. 〘 名詞 〙 確率変数Ｘのとる値に対しその値をとる確率を対応させたものをＸの確率分布という。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

確率分布 (かくりつぶんぷ)
probability distribution

実数値をとる確率変数Xに対してF（x）＝P（X≦x）とおき，これをXの分布関数という。それは，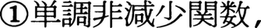

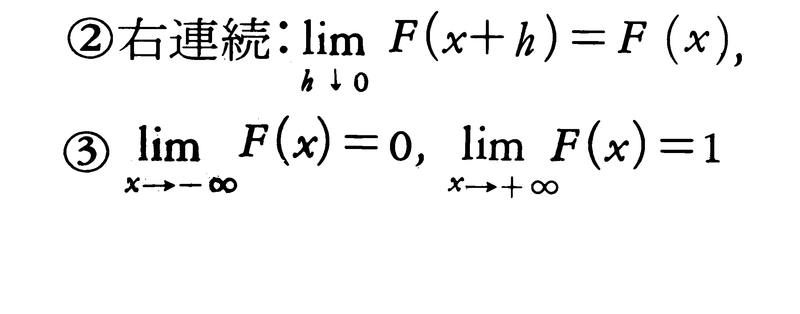
である。このようなF（x）があるとき，区間I＝（a，b］に対して集合関数Φ（I）＝F（b）－F（a）を定め，これを実数R上の測度にまで拡張したものをXの分布，または確率分布という。逆に，R上のΦ（R）＝1である測度，すなわち確率測度が与えられると，分布関数F（x）＝Φ（（－∞，x］）が一意的に対応し，それはある確率変数の分布関数となる。任意の分布関数F（x）はつねにF（x）＝a₁F₁（x）＋a₂F₂（x）＋a₃F₃（x），a₁，a₂，a₃≧0，a₁＋a₂＋a₃＝1と分解される。ここで，F₁，F₂，F₃はそれぞれ分布関数で，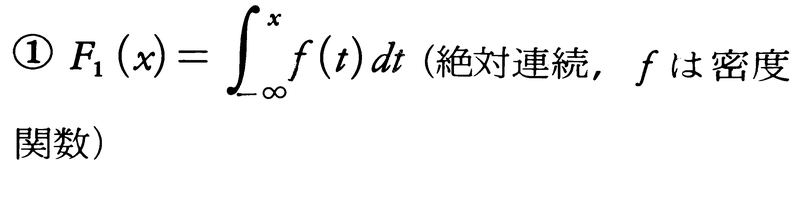

　　　（2）F₂（x）は階段関数，（3）F₃（x）はxの連続関数であるが絶対連続な成分はない。重要なのはF₁とF₂で，F₁は連続型，F₂は離散型であるという。

離散型分布

（1）もっとも重要なものは二項分布であり，F（x）はx＝0，1，……，nのみで増加し，x＝kでの跳びは_nC_kp^kqⁿ⁻^k（q＝1－p）である。これは成功する確率がpであるn回のベルヌーイ試行における成功する回数の分布である。

（2）ポアソン分布　Xは0，1，2，……の値をとり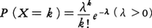，のとき，この分布がポアソン分布である。実例としては，電話のコールの回数とか放射性物質の崩壊など一定時間区間内に起こる回数の分布がある。二項分布も，nが大きく，pが小さくてnpがふつうの大きさのときnp＝λとしてポアソン分布で近似される。

（3）幾何分布　ベルヌーイ試行で成功するまでの回数をXとすればP（X＝k）＝q^k⁻¹p（k＝1，2，……）で，これが幾何分布である。

（4）壺の中にn₁個の赤球，n₂＝n－n₁個の黒球がある。この壺からかってにr個選んだときそのうちのk個（0≦k≦r）が赤球である確率q_kは

　　

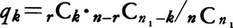
となる。これを超幾何分布という。

連続型分布

（1）もっとも重要なものはなんといっても正規分布（ガウス分布）である。平均値がm，分散σ²のとき，その密度関数は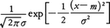，で与えられる。この分布は誤差論で支配的な役割を果たすほか，多くの自然現象にも現れ，中心極限によって分布の極限としてもとらえられる。m＝0，σ²＝1のとき標準正規分布という。

（2）X₁，X₂，……，X_nを標準正規分布に従う独立な確率変数とすれば，X₁²＋X₂²＋……＋X_n²は自由度nのΧ²分布に従う。それは密度関数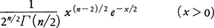，をもつ分布である。

（3）X，Yを独立で，それぞれ標準正規分布，自由度nのΧ²分布に従う確率変数とするとき，X/（Y/n）の分布を自由度nのt-分布という。その密度関数は，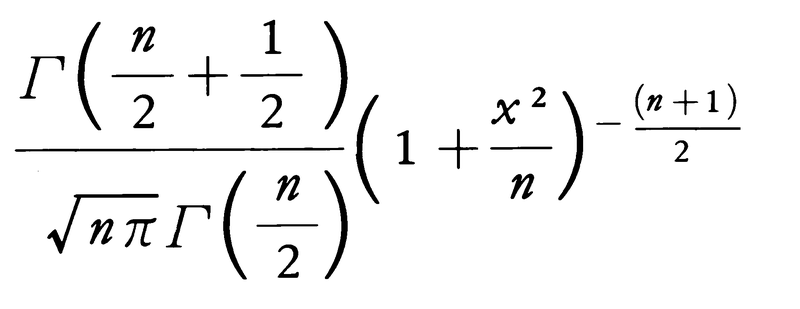

である。

（4）Γ分布はその密度関数が正のパラメーターλとrにより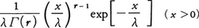，と表されるもの，またワイブル分布は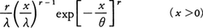，を密度関数にもつもので，ともに応用上しばしば用いられる。とくにr＝1のときのΓ分布は指数分布と呼ばれる。

（5）コーシー分布　図のようにルーレットが止まったとき，針の先の示す直線上の点はコーシー分布に従って分布する。その密度関数は，

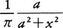　である。

多次元の場合

n次元空間Rⁿ上の分布関数は，（1）任意の正数h₁，h₂，……，h_nに対して，F（x₁＋h₁，x₂＋h₂，……，x_n＋h_n）－F（x₁，x₂＋h₂，……，x_n＋h_n）－……－F（x₁＋h₁，……，x_n-1＋h_n-1，x_n）＋……＋（－1）ⁿF（x₁，x₂，……，x_n）≧0，（2）各変数について右連続，（3）少なくとも一つの変数が－∞に近づくとき→0，すべての変数が→∞のとき1に近づくの諸性質を満たすものである。正規分布はとくに重要で，その密度関数は，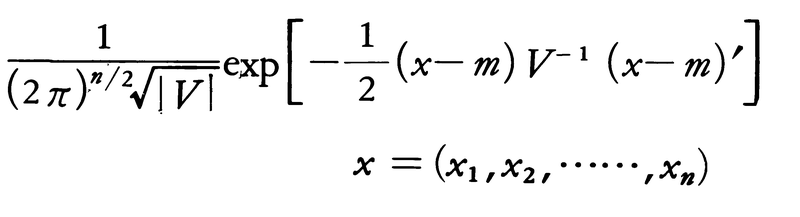

である。ただし，mは平均ベクトル，Vは共分散行列（正定値である），V⁻¹はVの逆行列，x－mと（x－m）′はそれぞれ横および縦ベクトルを表す。
執筆者：飛田 武幸

図－確率分布

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

確率分布
かくりつぶんぷ

確率変数Xが与えられると、任意の区間Iに対して、Xの値がIに属する確率Φ(I)＝P(X∈I)が決まる。このΦをXの確率分布、または単に確率分布という。確率分布のうちでとくに重要なものは二項分布、ポアソン分布、正規分布である。これらについてはそれぞれの項目をみられたい。

　たかだか可算集合A＝｛a₁,a₂,……｝において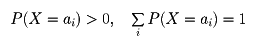

であるような確率分布を離散分布という。また、有限個の点を除いて連続な関数f(t)≧0があって、任意の実数xに対して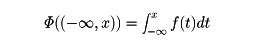

が成り立つとき、この分布を連続分布といい、f(x)を確率密度または密度関数という。

　以下、確率分布の例をあげる。

(1)一様分布　確率変数Xのとる値が有限個であって、どの値をとる確率も等しいとき、すなわち、a₁、a₂、……、a_nを相異なる実数として、P(X＝a_i)＝1/n(i＝1,2,……,n)のとき、Xの確率分布を離散型の一様分布という。

(2)超幾何分布　赤球がn個、黒球がN－n個入っている袋の中からr個の球を取り出したとき、そのなかに含まれている赤球の個数をXとすると、Xの確率分布は次式で与えられる。

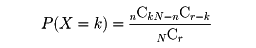
ただしkは0≦k≦n、0≦r－k≦N－nの範囲を動くものとする。この確率分布を超幾何分布という。この名称は、級数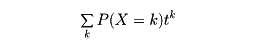

が超幾何級数で表されることに基づく。

(3)パスカル分布・幾何分布　ある試行において事象Eのおこる確率をpとする。この試行を独立に繰り返すことにして、事象Eがr回おこるまでにEがおこらなかった回数をYで表すと、Yの確率分布は、q＝1－pとして
　　P(Y＝k)＝_r-1+kC_kq^kp^r (k＝0,1,2,……)
となる。この確率分布をパスカル分布という。とくにr＝1の場合を幾何分布ということもある。

(4)負の二項分布　前記のパスカル分布においてrは正の整数であった。rを正の実数αとした場合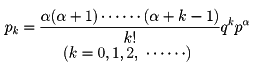

で与えられる確率分布を負の二項分布という。この名称は、各項が指数が負である場合の二項展開から得られる級数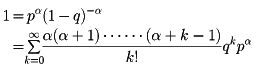

の各項になっているからである。

　前記の例(1)～(4)は離散分布である。次に連続分布の例をあげる。

(5)一様分布a＜bとして、確率密度が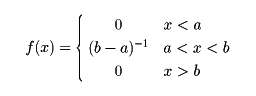

で与えられる分布を連続型の一様分布という。

(6)コーシー分布　確率密度が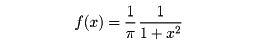

で与えられる分布をコーシー分布という。

(7)指数分布　確率密度が
　　f(x)＝(1/2)e^-|x|
で与えられる分布を指数分布という。

(8)ガンマ分布　λ＞0,α＞0として、確率密度が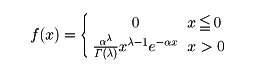

で与えられる分布をガンマ分布という。ここでΓ(λ)はガンマ関数である。

(9)対数正規分布　確率変数Xの分布が正規分布N(m,σ²)であるとき、確率変数Y＝e^xの分布を対数正規分布という。確率密度は次の式で与えられる。

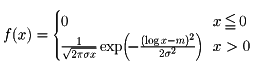
（ただしexpAはe^Aを表す）
この分布は所得の分布など経済統計に現れる。この分布をもつ母集団からの任意標本に対しては相乗平均が重要である。

(10)χ²分布、t分布、F分布　χ²分布はカイ二乗分布と読む。これらの分布については標本分布の項をみられたい。

　なお、前記(8)のガンマ分布において、nを正の整数としてλ＝n/2、α＝1/2と置いたものは自由度nのχ²分布である。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

確率分布
かくりつぶんぷ
probability distribution

単に分布ということもある。離散確率変数 X の分布を表示するには，

Pr{X＝x_i}＝f(x_i)　(i＝1，2，…)

を与えればよい。これを X の確率分布という。ここで Pr{X＝x_i} は，X が x_i ( i＝1 ，2，…) という値をとる標本点の集合，すなわち事象 X が X＝x_i という値をとる確率である。連続確率変数の場合には，確率密度によって示される。重要な確率分布には，二項分布，ポアソン分布，一様分布，正規分布などがある。

出典　ブリタニカ国際大百科事典 小項目事典