精選版 日本国語大辞典 「正規分布」の意味・読み・例文・類語
せいき‐ぶんぷ【正規分布】
日本大百科全書(ニッポニカ) 「正規分布」の意味・わかりやすい解説
正規分布
せいきぶんぷ
確率密度が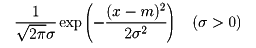
である確率分布を正規分布またはガウス分布という。正規分布の平均値はm、分散はσ2であり、特性関数はexp(imt-(1/2)σ2t2)である。この正規分布をN(m,σ2)と表す。とくに、m=0,σ=1の場合、すなわちN(0,1)を標準正規分布という。
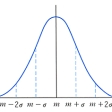
正規分布N(m,σ2)の確率密度を表す曲線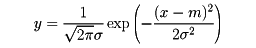
のグラフはのように、直線x=mに関して対称であり、x=mで最大値1/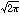 σをとり、x=m±σにおいて変曲点をもつ。確率変数Xの確率分布がN(m,σ2)であるとき、
σをとり、x=m±σにおいて変曲点をもつ。確率変数Xの確率分布がN(m,σ2)であるとき、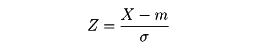
と置けば、Zの確率分布は標準正規分布となる。したがって正規分布に関する確率の計算は標準正規分布の場合に帰着される。すなわち、Xがaとbとの間にある確率は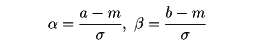
と置くと、Zがαとβとの間にある確率に等しい。すなわち、
P(a≦X≦b)=P(α≦Z≦β)この右辺の確率の値は正規分布表によって求めることができる。
確率変数Zの分布が標準正規分布であるとき、x≧0に対する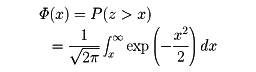
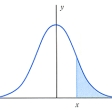
の値の表が作成されている。Φ(x)はの青色部分の面積を表している。この表を正規分布表という。
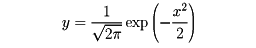
のグラフはy軸に関して対称であるから、正規分布表を用いると、与えられたα,β(α<β)に対してP(α≦Z≦β)の値を求めることができる。すなわち、
α<β<0のとき
P(α≦Z≦β)
=Φ(-β)-Φ(-α)
α<0<βのとき
P(α≦Z≦β)
=1-Φ(-α)-Φ(β)
0<α<βのとき
P(α≦Z≦β)
=Φ(α)-Φ(β)
二つの確率変数X1、X2が独立で、その確率分布がいずれも正規分布N(m,σ2)であるときc1X1+c2X2(c1、c2は定数)の確率分布はN((c1+c2)m,σ2(c12+c22))である。これは正規分布の一つの特性である。同一の分布関数F(x)をもつ二つの確率変数X1、X2が独立であってc1X1+c2X2の分布関数があるcに対してF(cx)となる場合、F(x)を安定な分布関数という。F(x)が安定な分布関数で分散が有限であれば、F(x)は正規分布の分布関数である。
n次元正規分布A=(aij)をn次正値対称行列、Δ=detAとして、n次元確率密度が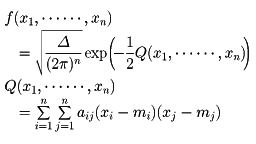
で与えられるn次元確率分布をn次元正規分布という。
正規分布の有名な実例をあげよう。ケトレーは成年男子の身長の分布が正規分布になっていることを確かめた。マクスウェルは気体分子の速度の分布が正規分布で表されることをみいだした。またガウスは偶然誤差の分布が正規分布であることをみいだした。正規分布に対するガウスの貢献によって正規分布はガウス分布ともよばれている。ポアンカレの著書『Calcul des probabilités』には誤差の分布についての観測と理論に関する興味深い記述がある。「実験家に聞けば、多くの場合正規分布に従うがそうでないこともある。そうでないのは観測が不十分であったためで、数学者が証明しているように当然正規分布に従うはずであると答える。また数学者に聞くと、それは数学的に確立されたのではない。実験によってそうなっているのだと答える」。この問題の数学的定式化は、20世紀に入って確率変数の和の問題について中心極限定理が確立されて初めて完成した。
[古屋 茂]
改訂新版 世界大百科事典 「正規分布」の意味・わかりやすい解説
正規分布 (せいきぶんぷ)
normal distribution
連続な確率分布のもっとも重要な例で,ガウス分布Gaussian distributionともいう。一次元の場合,その確率密度関数は,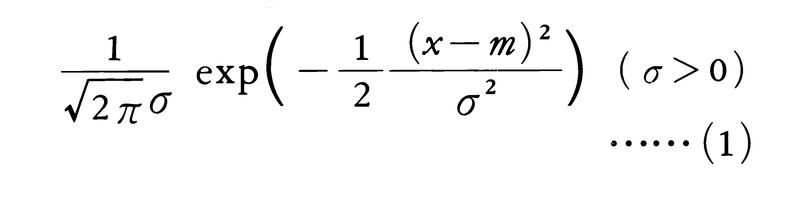
と表され,mが平均値,σが標準偏差である。とくにm=0,σ=1のとき標準正規分布という。諸量の測定誤差の分布が正規分布になることはよく知られている。また工学的機構から発生するノイズや生物的な現象に現れる“ゆらぎ”にも正規分布をなす例が多く,自然界の中に存在する分布である。また同種の独立な偶然量が多数加わったとき,それらの和を規格化したもの(平均値を引き去り標準偏差で割ったもの)は標準正規分布に近い。このように正規分布は具体的な背景をもっているばかりでなく,理論的にも著しい特徴をもつ分布である。正規分布に従う独立な二つの確率変数の和の分布は,また正規分布であるが,逆に独立な2確率変数の和が正規分布に従うなら,元の2変数はともに正規分布に従うことがわかる。またこの分布は平均値mと標準偏差σが決まれば(1)によって一意的に決まってしまう。いま,この分布に従う変数がある値aをとったとすれば,(a-m)/σ=a′の値を標準正規分布の表と比較してその位置づけがわかる。例えばa′が1,1.65,3をこえる確率はそれぞれ約0.16,0.05,0.001である。
二次元正規分布の密度関数は,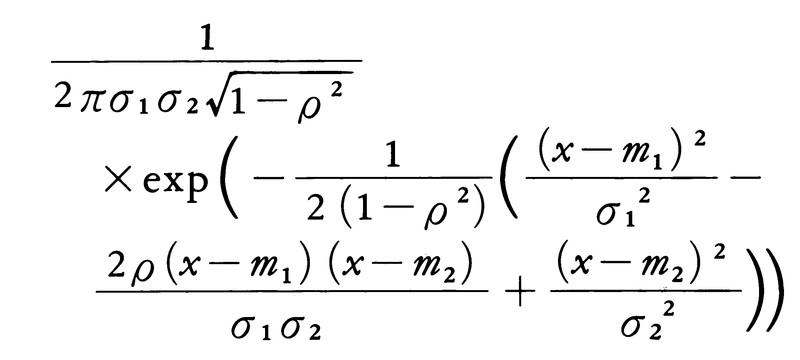
である。ここでρは相関係数を表す。xがある決まった値aをとったとき,yの条件付き確率分布もやはり一次元正規分布で,その条件付き平均値はaの一次関数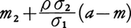 となる。正規分布から派生する分布で重要なものとして,χ2分布,フィッシャーのz分布,β分布などがあり,数理統計学においてたいせつな位置を占めている。
となる。正規分布から派生する分布で重要なものとして,χ2分布,フィッシャーのz分布,β分布などがあり,数理統計学においてたいせつな位置を占めている。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「正規分布」の意味・わかりやすい解説
正規分布
せいきぶんぷ
normal distribution
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「正規分布」の意味・わかりやすい解説
正規分布【せいきぶんぷ】
→関連項目F分布|ガウス|確率誤差
出典 株式会社平凡社百科事典マイペディアについて 情報
最新 地学事典 「正規分布」の解説
せいきぶんぷ
正規分布
normal distribution
本質的に連続するデータを統計的に扱う際に用いる分布の型。ガウス分布とも。観測値をx, 平均値をμ,標準偏差をσとすると,確率密度yはy=(1/(σ(2π)1/2))exp{-(x-μ)2/2σ2}なる関数に従い,μに関して対称なベル形をなす。分布の約68%がμ±σに,約95%がμ±2σに,約99.7%がμ±3σに入る。
執筆者:日下部 実
出典 平凡社「最新 地学事典」最新 地学事典について 情報
法則の辞典 「正規分布」の解説
正規分布【normal distribution】
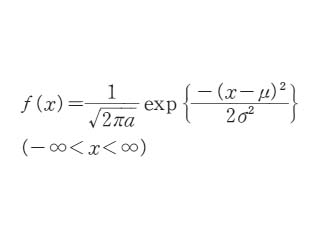
ブランド用語集 「正規分布」の解説
正規分布
出典 (株)トライベック・ブランド戦略研究所ブランド用語集について 情報
栄養・生化学辞典 「正規分布」の解説
正規分布
世界大百科事典(旧版)内の正規分布の言及
【確率分布】より
…これを超幾何分布という。
[連続型分布]
(1)もっとも重要なものはなんといっても正規分布(ガウス分布)である。平均値がm,分散σ2のとき,その密度関数は,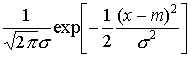 で与えられる。…
で与えられる。…
※「正規分布」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
1 花の咲くのを知らせる風。初春から初夏にかけて吹く風をいう。2 ⇒二十四番花信風...


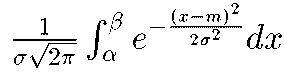 に等しいとき、Xは
に等しいとき、Xは