改訂新版 世界大百科事典 「数学パズル」の意味・わかりやすい解説
数学パズル (すうがくパズル)
mathematical puzzle
数学的な側面を多少でももったパズルを総称して,数学パズルという。ふつうは,題材が数学的であったり,解き方が数学的であったり,解答が数学的であったりするが,ほかにもマッチ棒のパズルや迷路のパズルなど,数学パズルに含まれるものは多い。数学パズルの特徴は,予備知識なしにだれにでも簡単に取り組むことができ,しかも頭のレクリエーションとして,楽しいひとときを思わず過ごすところにある。これはすべてのパズルに共通し,クロスワードパズルやジグソーパズルについてもいえる。しかし,知識の有無を問題にするクイズとは明確な一線を画する。例えば,西郷隆盛は何歳で死んだかという問題はクイズである。彼の没年を知っていれば答えられ,知らなければ答えられない。これに対し,ぼくの父の歳を3で割ると1余り,4で割ると2余り,5で割ると3余る。父は何歳かという問題はパズルである。その歳を知らなくても,あれやこれやと考えているうちに,いつしか正解にたどり着く。また,たどり着けなくても58歳という正解を聞けばなるほどとうなずける。このとき,考え方は直観であっても,ひらめきであっても,推理であっても,しらみつぶし的な調査であっても,数学で解いてもいい。解き方を制限しないところに数学パズルのおもしろさがある。
数学パズルの発祥は古く,前16世紀ころに書かれたエジプトの数学の記録,アアフメスの《リンド・パピルス》にも数学パズルの記載がある。これから推すと,数学の誕生とほぼ同時に数学パズルも生まれているらしい。しかし,数学パズルとしての独自の認識がもたれたのは15~16世紀のころで,世界最初の本格的な数学パズルの専門書は17世紀の初期に刊行されている。これは,フランスの数学者バシェC.G.Bachet,Sieur de Meziriac(1581-1638)著の《愉快で楽しい問題》(1612)で,百五減算や魔方陣の作り方などを含めて40題を収録している。日本では,田中由真(1651-1719)著の《雑集求笑算法》(1698)がもっとも古く,小町算や目付字などを含めて22の題材を扱っている。この本は,日本の古典パズルの教典である《勘者御伽双紙》(1743)の種本であることが最近判明した。また,次に古い《和国智恵較》(1727)では,10種の楽しい絵入りの問題を出題している。このように,17世紀ころから本格化してきた数学パズルはその後に急速な発展をなし,20世紀の今日では成書や雑誌,パズル具などがたいへんなはんらんぶりを見せている。しかも,初期のころは油分け算や継子立てのような算術パズル,碁石拾いや図形の裁ち合せのような幾何パズルが主だったが,現在では電卓やマイコンを指向したものまで,さまざまな数学パズルが考えられている。
それゆえ,ひと口に数学パズルといっても,そこで扱う題材と内容は千差万別であり,これを体系的に分類するのは困難である。いま数学の分野に応じておよその分類をすると,(1)算術パズル,(2)代数パズル,(3)幾何パズル,(4)トポロジーパズル,(5)組合せパズル,(6)論理パズル,(7)その他となる。微分積分や関数方程式のパズルがないのは,これらの数学が庶民的なパズルには不向きのためである。また数学パズルの中には特定の題材を中心にして大きな発展をなし,それだけで一分野を作っているものがある。それには,虫食算と覆面算,魔方陣と星陣,ポリオミノとポリアモンド,迷路が含まれる。一方,数学パズルの中には道具を使うものも多く,それで分類すると,(1)日用品を利用するパズル,(2)ゲームに関連するパズル,(3)特殊の用具を使用するパズルとなる。以下では代表的な数学パズルを紹介しながら,これらについての概略を展望をする。
算術パズル
大英博物館所蔵の《リンド・パピルス》には,次のような意味の数学パズルが記載されている。〈7軒の家で7匹ずつの猫を飼っている。それぞれの猫は7匹ずつのネズミをとる。それぞれのネズミは7本ずつの麦の穂を食べる。それぞれの麦の穂からは7ますずつの麦がとれる。これらの数をみな合わせるといくらになるか。答えは19607〉。このように数字のおもしろさや計算の楽しさをねらったものが算術パズルである。図1-aはリュカM.E.Lucas(1842-91)著の《数学遊戯》第4巻(1894)に紹介されたもの,図1-bはフォーリーE.Fourrey著の《算術遊戯》(1899)に紹介されたもので,その楽しさはひと目でわかる。この種の算術パズルはかなり古くから存在していたが,その発祥は不明である。同じ趣旨の算術パズルとしては日本の小町算が有名である。田中由真著の《雑集求笑算法》に最初の紹介があり,出題に〈通小町九十九夜〉という名がつけられている。これを中根彦循(1701-61)著の《勘者御伽双紙》上巻(1743)が小町算として引用し今日に至っている。小町算の内容は,1から9までの9個の数字,または0から9までの10個の数字を使って,いろいろの数やおもしろい数式を作ることである。図2はその代表的なもので,図2-aは1から9までの9個の数字の間に+と-の記号を入れて100とし,図2-bは1から9までの9個の数字で分数式を作っている。同じ楽しさをねらったものには四つの4もある。ボールW.W.R.Ball(1850-1925)著の《数学遊戯とエッセー》(1914)に紹介があり,問題自身は以前からあったとの記事がある。4個の4と数学の記号を使って,なるべく多くの数を表そうというものである。図3はその例で,0から10までの数を+,-,×,÷,かっこの記号で表している。むずかしい記号を使うほど大きい数まで表せるが,小さい数では113と157が比較的作りにくい。小町算や四つの4を見ると,似たような算術パズルはいくらでも作れることがわかる。事実,数作りとか数楽とかいって,今日でも西暦の年などを使った算術パズルがいろいろ考えられている。
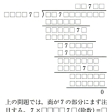
算術パズルの中では,虫食算が一つの分野を作っている。和紙が虫に食われやすいことに着目して,加減乗除の計算に欠落個所を作ったパズルである。図4は藤田貞資著の《精要算法》(1781)にある代表的な虫食算であるが,最初に紹介したのは久留島義太著の《算梯》(稿本のため年代不詳)であるらしい。今日の虫食算は図5-aのような形態となり,小学生や中学生でも取り組めるようになっている。なお図5-bは〈孤独の7〉と呼ばれる有名な虫食算で,解くのに多少の着想がいる。コンピューターなどを使うと,いくらでもむずかしい虫食算が作れるが,解が一つだけということが作成の絶対条件となる。
代数パズル
出題や解法に代数的な要素を含んだ数学パズルで,算術パズルとの明確な区別はつけにくい。最古の数学パズル書と見られる,バシェ著の《愉快で楽しい問題》には多くの代数パズルがあり,その中には百五減算の原形である六十減算や油分け算も含まれている。百五減算は吉田光由の《塵劫記》下巻(1631),中根彦循の《勘者御伽双紙》上巻にも紹介されており,相手の年齢を当てるパズルである。今,相手の年齢を3,5,7で割ったときの余りを尋ね,その返事がa,b,cであったとする。これから70a+21b+15cを計算し,その値が105より大きいときは,105を何回か引いて105以下にする。その値が相手の年齢である。この種は70,21,15にあって,例えば70は3で割ると1余り,5と7では割り切れる数に選んである。当てるということでは目付字も同じである。《塵劫記》や《雑集求笑算法》などの多くの和算書に紹介されているが,図6-aは《勘者御伽双紙》下巻に載っているもので,この中の一つの文字を相手に思わせる。これが〈と〉であったとしよう。次に5本の枝のそれぞれについて,花にあるか葉にあるかを尋ねる。この場合は上から2番目と3番目の枝では花,その他の枝では葉である。すると図6-bの指示に従って花にある枝の数を加える。8+4=12である。最後に〈さくら木の ふみやいづれと おぼろげも はなにありしを かずえてぞうる〉という和歌を読み,その12番目の〈と〉を当てる。和歌が解き方の説明であると同時に実際の鍵にもなっているところがおもしろい。この変形は西洋の数学パズルにも存在し,すでにバシェ著の《愉快で楽しい問題》にはトランプの並べ替えによる当て物が紹介されている。目付字は二進数を利用したもので,この発想は古くからあったようである。代数パズルとしては継子立ても有名である。図7-aは《塵劫記》下巻にあるもので,内容は次のようである。子どもが30人いて,そのうちの15人は先妻の子,残る15人は自分の子である。30人を図7のように並べ,10番目ずつに当たる子どもを除いていって,最後に残った子どもに家督をゆずることにした。図7-bでは,継子を○,実子を●として見やすくしてある。こうして数え始めると,継子ばかりが次々と抜けていった。あと1人で継子がいなくなろうとしたとき,最後の継子がいった。これでは継子ばかり抜けて不公平だから,今からは自分から数えてくれと。しかたなくそうすると,今度は実子ばかり抜けていって最後に継子が残ってしまった。継子立ての記述は吉田兼好の《徒然草》にもあるから,かなり古くから知られていたらしい。また西洋ではジョセハスの問題として,その研究は4世紀までさかのぼれるという。しかし正確なところは不詳である。
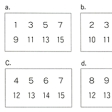
代数パズルはこのほかにもたくさんあるが,覆面算は虫食算と並んで一分野を作っている。計算の中の数字を文字に置き換えたもので,各数字ごとに別の文字を割り当てている。図8-aは有名な覆面算で,どの本にも引用されている。図8-bは最近作で,単語の意味でも数式を作っている。コンピューターはこのような覆面算の制作に強力で,うまく文字を割り当てれば図8-cや図8-dも簡単に作れる。なお覆面算と虫食算を合わせたような図8-eの変種もある。覆面算や虫食算はコンピューターの出現で急速な進歩を遂げたが,反面,手作りの楽しさが失われてきつつある。
幾何パズル
図形に関するパズルが幾何パズルである。図9-aは環中仙(生没年不詳)著の《和国智恵較》(1727)にあるもので,長方形を正方形に裁ち合わせる方法を尋ねている。図9-bはその解で,単純ながら幾何パズルの性格をよくとらえている。また図10-aはリュカ著の《数学遊戯》第2巻にあるもので,左の正方形を右の長方形に組み替えると,面積が小さい正方形の1個分だけ多くなってしまう。しかし長方形を拡大しながら正確にかくと,小さなすき間が図10-bのようにできている。このように幾何パズルには視覚でとらえられるものが多いので,数学的に凝ったものでも不自然さが現れにくい。図11-aは平行四辺形を正方形に裁ち合わせるもの,図11-bは正方形を正五角形に裁ち合わせるもので,どちらもリュカ著の《数学遊戯》第2巻に紹介されているが,その数学的な内容には深みがある。また図12はデュードニーH.E.Dudeney(1847-1930)著の《カンターベリー・パズル》(1919)に紹介されているもので,正方形から正三角形への裁ち合せを与えている。しかも鳩目(はとめ)でつないだ4片を右に回せば正方形,左へ回せば正三角形という驚異的なものである。デュードニーは世界最大のパズリストといわれた人で,このような幾何パズルの名作をいくつも作っている。風変りな幾何パズルとしては,ルージンN.N.Lusin(1883-1950)の問題と呼ばれるものがある。一つの大きな正方形を大きさの異なる小さな正方形で埋め尽くす問題で,当のルージンは不可能であろうと予想した。図13-aのようにすると正方形ができそうであるが,惜しいところで長方形になっている。この問題はケンブリッジ大学の学生だったタットW.T.Tutteと3人の同級生によって1940年に理論的に解決され,大きな話題をまいた。図13-bは具体的な埋尽しの一例である。幾何パズルはほかにもいろいろあり,例えば図14の星形と奇妙な回転のこぎりの歯は,1辺の長さが120の正六角形と正十一角形の各辺に大きさの違う直角三角形をつけ,すべての辺の長さを異なる整数になるようにしている。ピタゴラスの定理のみごとな応用である。
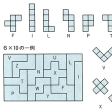
ポリオミノとポリアモンドは幾何パズルの一分野を作っている。ポリオミノは同じ大きさの正方形をいくつかつないだもの,ポリアモンドは正三角形をつないだもので,例えば5個の正方形をつないだペントオミノは図15-aの12種類,6個の正三角形をつないだヘクサモンドは図15-bの12種類となる。この12種類を箱詰めにするとおもしろいパズルができ,図15-cの6×10の長方形にペントオミノを入れると3776通りの入れ方がある。
トポロジーパズル
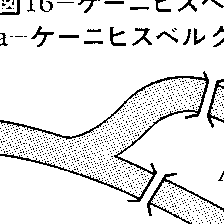
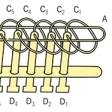
点と線のつながり方を問題にするのがトポロジーパズルで,数学者のL.オイラーが1735年に提案した一筆書きの問題が最初である。ドイツのケーニヒスベルクは古い都で,18世紀の初めころは七つの橋が図16-aのようにかかっていた。このすべての橋を一度ずつ渡るコースがあるかというのが問題で,実は存在しないのである。オイラーは川で仕切られた四つの地域を点に替え,橋を線に替えて図16-bを作り,この上での一筆書きを調べた。すると各点から3本,または5本の線がでていてすべて奇数である。オイラーは奇数の点が2個か1個もない場合だけ一筆書きができることを証明した。図17-aはアーレンスW.Ahrens著の《数学遊戯》第2巻(1918)にある問題で,かなり複雑そうに見えるけれども,A点とB点だけが奇数の点であることを確認すれば図17-bのような解が簡単に得られる。一筆書きと似たトポロジーパズルにハミルトン閉路の問題がある。W.R.ハミルトンが考えたもので,その結果を1859年に報告している。この問題は図18-aの正十二面体の稜を伝わって,20個の頂点を一巡するコースを求めよというものである。等価な問題の図18-bに直すと,実線で示した一巡コースが得られる。図19-aはデュードニー著の《数学の楽しみ》(1917)に紹介されているもので,すばらしい着想のパズルである。まず,味方のBが1駒追いかけ,次に敵のEが1駒逃げる。こうして交互に1駒ずつ移動したとき,どうすれば敵をつかまえられるかというものである。その方法は予想外で,敵の動き方に関係なく(1)の地点を通るようにすれば,敵が(1)の地点を通らないかぎり成功する。例えば図19-bの太線のコースを進むと,敵が(1)の地点を通ればその直後に成功し,通らなければみかたが(1)の地点を通った後に成功する。実際に試すとおもしろさが理解できる。
迷路はトポロジーパズルの一分野を作っており,視覚だけで楽しめるので週刊雑誌などに盛んにでてくる。迷路の歴史は古く,9世紀以前にはキリスト教国の皇帝が着る礼服の装飾に用いられ,まもなく大聖堂や他の教会の装飾として採用されるようになった。図20-aはロンドン郊外にあるハンプトン・コートの迷路で,ウィリアム3世の楽しみのために1690年に作られた。また図20-bはフランスのサン・ベルタン寺院の廃墟にある迷路である。今日では紙上での各種各様の迷路パズルが考案されている。
組合せパズル
いろいろの組合せ方を問題にするのが組合せパズルで,すでにバシェ著の《愉快で楽しい問題》には,川渡りのパズルが紹介されている。3組の夫婦が川を渡りたいが,船は2人乗りが1そうしかない。しかも夫婦が分かれているときに夫が他の夫人といっしょにいると何をするかわからない。どうすれば安全に渡れるかという問題である。3組の夫婦をAとa,Bとb,Cとcとすると,図21がその解となる。カークマンT.P.Kirkman(1806-95)は1847年に15人の女生徒の問題を提案し,その3年後に解を示している。15人が3人ずつの5組に分かれて学校に1週間通い,どの人も他のすべての人と1回ずつ同じ組に入るようにせよというものである。15人をaからoまでとすると図22が一つの解となる。この問題は女生徒の数を6人ずつ増やしていっても解くことができる。またリュカ著の《数学遊戯》第2巻ではリーグ戦の組合せの問題を紹介し図23の解を与えている。これはAからLまでの12人が2人ずつの6組に分かれ,テニスのような試合を同時に行ったとき,11回の組替えでどの人も他のすべての人と当たるようにせよという問題である。図23-aの弦で結ばれた2人ずつが1回目の試合をすると,残りの試合は外側の11人を順次に回転させただけで得られる。図23-bはこの方法による具体的な組合せを示す。これを知らないとなかなか解けない問題で,実にみごとな解である。組合せパズルの20世紀の傑作としては,1945年の数学雑誌に載った贋金(にせがね)の鑑定問題がある。見かけ上は完全に同じコインのうちに贋金が1枚だけある。そのコインは本物と違って重いか軽いかわからないけれども目方が少し違う。これをてんびんに3回かけるだけで見つけだせというのである。この見つけ方はいろいろあるが,図24の方法がもっともすばらしい。玉の番号を1から12までとし,てんびんの左の皿に乗せる玉を+,右の皿に乗せる玉を-,どちらの皿にものせない玉を○とし,1回目から3回目までの乗せ方を図24-aのように決める。左右の皿に乗せる玉は4個ずつである。その結果,てんびんの傾きが左であれば+,右であれば-,つりあえば○とする。例えば1回目が-,2回目が○,3回目が+とすれば,図24-bのような表を作る。これと図24-aを比べ,一致している7番目の玉を贋金と見破るのである。
これまでに見てきたように,組合せパズルはどちらかというと高級なものが多い。デュードニーの著書にはさらに高級なパズルが紹介され,その中には今日まで未解決の円卓問題や高等数学を必要とする囚人の手鎖問題などが含まれている。
論理パズル
三段論法のような論理を使うパズルが論理パズルである。クライチックM.Kraichik著の《数学遊戯》(1942)には,いろいろのおもしろい論理パズルが載っている。その中のうそつき島の話は秀逸である。ある離れ島の原住民はA族とB族の2部族に分かれており,A族はつねに真実を話すが,B族は必ず真実の逆をいうという。ある探検家がこの島を訪れ,3人の原住民に出会った。最初の人に君はどちらの部族かと尋ねたところ,原地語で答えたため理解できなかった。すると英語を少し話せる2番目の人は,彼はA族に属するといったといい,3番目の人はB族に属するといったという。2番目と3番目の人で,どちらがうそをついているか。最初の人がどちらの部族かわからないので判定がつかないように見えるが,どちらの部族に属していてもA族に属しているというのである。A族ならば真実を話し,B族ならば真実の逆を話すからである。問題のおもしろさはここにある。論理パズルでは,いろいろなヒントから犯人を捜し当てたり,10人くらいを夫婦のカップルに組み分けたりする問題が多いが,ノーベル物理学賞を受けたP.A.M.ディラックの作といわれる次のパズルは最高の傑作である。いろいろの形で紹介されているが,帽子の例はわかりやすい。3人の死刑囚に3個の白い帽子と2個の黒い帽子を見せ,この中の3個を君たちの頭にかぶせるが,自分のが白い帽子と確信したら逃げだしてよい。しかし黒い帽子だったらその場で射殺するという。そして見えないように3人に白い帽子をかぶせ,2個の黒い帽子はすばやく隠してしまう。囚人たちは他の2人の帽子は見られるが,自分のは見えない。3人はしばらく考えていたが,やがていっせいに逃げだしたという。どうして自分の帽子が白いと確信したのか。まず2人の帽子が黒ければ,もう1人は直ちに逃げだす。そこで自分の帽子が黒いと仮定してみる。すると2人のうちのどちらかは,もう1人が直ちに逃げださないことから自分の帽子が白いことに気づき,逃げだすはずである。しかし2人とも逃げださないから,自分の帽子は白いに違いない。3人はこれに同時に気がついていっせいに逃げだしたのである。みごとな推理で,説明されてもわかりにくい面がある。図25は図形を利用した論理パズルなので,奇妙な論理であるがわかりやすい。図の1列目には5個の図形が並んでいる。この中で違う図形は左端の三角形である。2列目には2個の正三角形と3個の正方形があるが,点線でかかれているのは中央の正方形だけである。3列目では右から2番目の図形だけが×印で,あとは○印であるからこれが違っている。では4列目はどの図形が違っているか。左端は三角形だから他と違っている。左から2番目は中が×印だから他と違っている。中央は外側が点線だから他と違っている。右端は中が◎印だから他と違っている。しかし右から2番目は他と違っている点がない。つまり他と違っている点がないということで他と違っているのである。死刑囚の帽子の問題とどこか似ている点がある。
日用品を利用するパズル
日用品を利用するとおもしろいパズルがいろいろできるので,そのいくつかを紹介する。図26は下駄の縄抜けパズルで,多くの本にいろいろの形で紹介されている。図27はコインのパズルで,6個で正六角形を作れというものである。ただし机上から持ち上げてはいけないという条件があり,図27-bの方法は許されない。このため図27-cの解を見ると飛躍した発想が使われている。図28はマッチ棒のパズルで,図28-aではマッチ棒の移動を問題にしている。横に並んだ10本のマッチ棒を次の規則で移動させ,2本ずつの5組にできれば成功である。その規則とは,どのマッチ棒でもいいから右か左へ2本を飛び越して3本目に重ねるというものである。ただし重ねられた2本のマッチ棒を飛び越すときはそれを2本と数え,いったん重ねられたマッチ棒は二度と離さないものとする。このパズルは8本以上なら何本のマッチ棒でもできる。図28-bはマッチ棒で橋を作るもので,接着剤を使ってはいけない。マッチ棒による組立てパズルはほかにもいろいろ考えられている。しかし日用品を利用するパズルには伝聞によるものが多いため,その発祥を調べるのは困難である。このことは次のゲームに関連するパズルについてもいえる。
ゲームに関連するパズル
ほとんどのゲームに関連してパズルが考えられている。図29は将棋の馬鹿詰めと呼ばれるパズルで,最少手数の勝負を示している。もちろん先手は早く勝つように指し,後手はそれに協力して早く負けるように指す。わずか7手で詰む手順がほかにもいくつかある。馬鹿詰めはほかのゲームでもある。図30はオセロに対するもので,先手が勝つ9手の手順と後手が勝つ10手の手順が示してある。どちらも一方の石だけになり,規則によって相手は打つことができなくなる。碁石によるパズルとしては,テートP.G.Tait(1831-1901)の飛石問題が有名である。1884年に発表したもので碁石の移動を問題にしている。白石と黒石を交互に横に並べ,図31の最上段のようにする。ここでは4個ずつであるが,3個ずつ以上の同数であれば何個ずつでもよい。次に隣り合ったどれか2個の石を,同時に右か左の空いているところへ移す。この操作を何回かやって,左右に白石と黒石がそろえば成功である。4個ずつのときは4回の操作,5個ずつのときは5回の操作というように,石の数と同じ回数の操作でいつでも並び替えることができる。チェスに関連したものとしては,8個のクイーンとナイトの周遊が有名である。チェス盤に8個のクイーンを置いて,お互いに効き筋にないようにするのが8個のクイーンの問題である。クイーンは将棋の飛車と角行を合わせたようなもので,縦横と斜め方向に自由に進める。図32は一つの解で,アーレンス著の《数学遊戯》第1巻には12種92通りのすべての解が示されている。ナイトは図33-aの八方に跳べる桂馬で,チェス盤のすべてのますを一巡するのがナイトの周遊である。図33-bはその一つの解で,コワレフスキーG.Kowalewski(1876-1950)著の《最新高等数学遊戯》(1930)にはこれの詳しい解析がある。
特殊の用具を使用するパズル
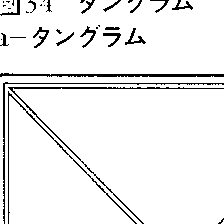
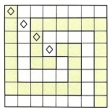
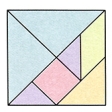
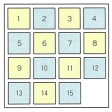
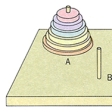
パズルのために作りだした特殊の用具も少なくない。図34はタングラムとその作品で,古くから中国で親しまれていたものが,19世紀前半に西洋に伝わっている。これと同系列のものには図35のクロス・ブレーカーがあり,日本でもタングラムと似た用具を解説した《清少納言知恵の板》(1742)という本が発見されている。図36-aの九連環は9個の環から棒を抜く知恵の輪パズルで,発祥はやはり中国である。早くから西洋に伝わったようで,チャイニーズ・リングと呼ばれ,16世紀にはイタリアの数学者G.カルダーノが抜き取る手数を考察している。最低でも341手かかるため,環の数を減らしたものも発売されている。図37のハノイの塔はリュカの創案で,彼の著書《数学遊戯》第3巻にその紹介がある。小さい円盤の上に大きな円盤を乗せないようにしながら8枚の円盤をAからBに移すもので,補助としてCの棒も用いる。最少の手数は255手である。図38の15パズルも有名で,ロイドS.Loyd(1841-1911)の1878年の創案になる。15枚の番号札を滑らせながら並べ替えるパズルで,最初の配置に応じて可能な並べ替えと不可能な並べ替えの2通りの配置ができる。ロイドは不可能な並べ替えをそれと知らせずに懸賞問題にしたため,一時はたいへんな人気を呼んだ。しかし不可能であることの証明が発表されて熱はさめた。図39のソリテリアも有名なパズルである。図39-aの33ヵ所の穴のうち,中央の穴だけ残してピンを差し込んでおく。そして次の規則でピンを1個ずつ取り去り,1個だけにできれば成功である。その規則とは,縦または横の直線上にピンが並んでいて,すぐその隣の穴が空いているとき,図39-bのようにピンを飛び越して飛び越されたピンを取り去るというものである。成功するときは最後のピンを中央の穴に残すことができる。そして32個のピンをどこに差し込んでも,最後のピンを最初の配置で空いている穴に差し込むようにして,いつでもただ1本だけ残すことができる。図40の組み木パズルもおもしろい。どうして組み込んだかという問題であるが,解を見れば簡単である。また図41の組み木パズルはその組込み方が巧妙である。同じ形をした図41-aの6本の組み木を図41-bの形に組み込むもので,内部に空間のできない点がみごとである。ワイアットE.M.Wyatt著の《組み木のパズル》(1928)に紹介されているから古いもののようである。図42-aのルービック・キューブは用具パズルの20世紀の最大傑作といわれている。ハンガリーの建築家ルービックE.Rubikが考案したもので,図42-bの回転をいろいろな方向で行いながらどの面も同じ色にそろえる。回転の巧みなメカニズムで現代人の感覚にぴったりである。ルービックは1975年に原案を作ったが,製作面で手間がかかって78年の発売となった。これが爆発的な人気を呼び,一時は全世界をふうびした。
その他の数学パズル
これまで触れなかったパズルに確率パズルなどがあるが,注目すべきものが少なかったので割愛した。またマイコンの普及によって新しいタイプのパズルも開発されてきている。
最後に図5-a,の虫食算と図8,の覆面算の解をそれぞれ図43と図44に示しておく。
執筆者:中村 義作
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報