翻訳|magic square
精選版 日本国語大辞典 「魔方陣」の意味・読み・例文・類語
ま‐ほうじん‥ハウヂン【魔方陣】
改訂新版 世界大百科事典 「魔方陣」の意味・わかりやすい解説
魔方陣 (まほうじん)
magic square
日本では関孝和が単に方陣と名づけた。1,2,……,n2のn×n個の数を正方形に並べて縦,横,斜めの和を一定にしたものであるが,種々の特徴がある。五方陣でいえば図1-aのごとく中心格13に関して対称な2格の和(例えば17+9,3+23)がすべて定数26となるものを対称方陣という。図1-bのごとく外側の中3格が相対する格との和が定数26となるものを親子方陣という。図1-cのごとく対角線に平行な汎対角線(例えば14+16+23+5+7)がすべて定数65となるものを完全方陣という。このほかに八方陣で示すように相結,対称四和,フランクリン型などの性質がある。このようにいろいろの性質があるから作り方は一様でない。
四方陣
四方陣880とおりは和が17となる連結線の形によって12型に分類される。うち連結線が対称の4軸をもつものは図2の3型である。aを完全,bを対称と称する。左上隅より行と列とに番号1,2,3,4をつける。aは行と列を(2,3,4,1)(3,4,1,2)(4,1,2,3)に交換をしてもやはり完全方陣である。これを行列変換という。bとcとについても変換を見いだせる。またaの行に(1,2,4,3)の変換を行い,その後に列について同じ変換を行うと対称方陣となる。このようにしてa,b,cは相互に移ることができる。
五方陣
対称と親子の性質は五方陣の作り方に利用される。高木貞治は座標を使って桂馬飛びと斜め飛びの関係を明らかにして〈3で割り切れない奇数次の方陣を桂馬飛びで作れば完全方陣になる〉ことを証明した。
八方陣
もっとも変化に富んでいる。図3-aは完全,対称のほか相結,対称四和が成立する。相結とは任意の二方4格(例えば22+11+44+53)の和はどこでも130となる。中心に関して対称な4格の和(例えば22+25+40+43)はどこでも130となる。これを対称四和が成立するという。図3-bは相結,完全のほかフランクリン型が成立する。アメリカの政治家B.フランクリンが研究したもので,例えば55+7+9+57+8+56+58+10のように山の形に取った和が定和260となるものである。山は下向き,左向き,右向きでもよい。この八方陣はこのほかに上下,左右の半分も定和になる。
二重方陣
1892年にフランスのフロローFrolowが八方陣と九方陣を発表している。両方とも対称方陣である。図4の八方陣は縦,横,斜めは260となるほか各数の2乗の和はどこでも11180となる。二進法で説明される。
素数方陣
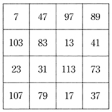
1900年ころからアメリカで素数ばかりで方陣を作ることが試みられた。いずれも連続した素数ではなかった。連続素数で方陣を作ったのは近年である。図5に五方陣(13~113)と六方陣(7~167)を示しておく。
立体方陣
1,2,……,n3のn×n×n個の数を立方体に組み重ねたもの。図6-aに示した立体三方陣は上面,中面,下面の縦と横合計18本,上下に貫く9本,立体対角線4本,総計31本がすべて一定数42になるもの。平面の対角線は必ずしも定数にならなくてよい。図6-bの立体四方陣はこの条件を満たすばかりでなく,最上面をそのまま最下面に移しても立体四方陣は成立する。また前後面,側面をはがして最後につけても同じである。立体四方陣の個数は不明であるが,完全立体四方陣の基本型は15とおりである。立体方陣の一隅から出る7本がみな定数となる理想的なものは立体七方陣で実現した。立体方陣も平面の場合と同様に,対称,相結などが考えられる。立体四方陣はP.deフェルマーが最初に作ったが,4本の立体対角線の成立するものは久留島義太が初めて作った。
歴史
中近東でもっとも古い方陣を集めたものに,989年ころのイスラムの百科事典がある。これには三方陣から九方陣まで17個伝わっている。四方陣では完全,対称,ほか一種がある。五方陣では対称,親子,完全(当然桂馬飛び)がある。六方陣から九方陣までは4軸対称となるものである。これから見ると一般の作り方が研究され相当のレベルに達したと思われる。16世紀になってドイツ,フランスで方陣の研究が起こり,1900年前後にアメリカで盛んになった。中国には楊輝の研究がある。楊輝の著書は南宋の1274-75年に完成したが,明の時代になって1378年《楊輝算法》として出版された。このなかの2巻が〈続古摘奇算法〉で方陣が含まれ,十方陣まで説明もなく並べてある。図7-aの七方陣は外側は対称型であるが,中は親子型である。図7-bの八方陣は対称型であり,4×4=16格の相結が成立する。格をジグザグに拾うと定和となるところが12ヵ所ある。例えば12+46+55+17+16+42+51+21=260などである。図7-cの十方陣では2×2=4格の相結とフランクリン型が成立する。実に楊輝の方陣は南宋の高度の文化を物語っている。日本に輸入された楊輝の方陣は,これらの特徴は忘れられた。日本では関孝和,安藤有益(1624-1708),田中由真(1651-1719)らの方陣の研究が著しい。みな親子方陣の一般的規則を与えたものである。久留島義太は桂馬飛びの方法と簡単な並べ方を,安島直円はフランクリン型を発見した。山路主住の五方陣,会田安明の四方陣変換の研究が著しい。
執筆者:平山 諦
中国
中国での歴史は古く縦横図とよばれた。最古の方陣は三次方陣の洛書数で,伝説上の帝王の禹が治水事業をしたとき,洛水から現れた亀の背に見られた文様が洛書数であったという(河図(かと)洛書)。中央の5は五行数に対応し宇宙を象徴する。《大戴礼(だたいれい)》明堂篇に294753618の数の記述があることなどから,前4世紀ころには三次方陣が存在していたとされる。《数術記遺》(2世紀末)に注を加えた南北朝期の甄鸞(しんらん)/(けんらん)は九宮つまり三次方陣を説明している。先にふれられている楊輝の〈続古摘奇算法〉には三から十までの方陣その他が扱われ,明の程大位の《算法統宗》にも14種の縦横図が載せられ,清の方中通の《数度衍》(1661)にも同様の方陣が見えるが多くは楊輝のものと同じである。日本の方陣研究は楊輝,程大位の影響のもとに江戸時代を通じて行われた。他方,中国では立体的な数の配列を研究した保其寿の《増補算法渾円図》があるほかは,見るべき成果はなかった。
執筆者:橋本 敬造
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「魔方陣」の意味・わかりやすい解説
魔方陣
まほうじん
magic square
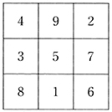
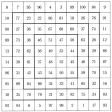
方陣ともいう。n×n個の升目に数を入れて、縦、横、斜め、どの1列のn個の数の和も一定になるようにしたもの。このnを次数といい、nが3なら三方陣、nが4なら四方陣というようによんでいる。二方陣はつくれないので、の三方陣が最小のものになる。三方陣には、「憎(にく)し(294)と思うな七五三(753)、六一(61)坊主にハチ(8)が刺す」などの覚え歌がある。また、1列の数の和は、1からn2までの数を入れた普通の魔方陣では、三方陣が15、四方陣が34、五方陣が65、六方陣では111、一般にn方陣ではn(n2+1)/2である。
魔方陣がいつごろからあったかは不明であるが、中国で古くから魔方陣が知られていたことは確かである。伝えによると、のちに夏(か)王朝の始祖となった禹(う)が、洛水(らくすい)という河の治水工事をしたときに、背中にのような模様のついた大きなカメが現れたという。この模様のひとつながりの丸を、それぞれの個数に相当する数に置き直してみると、の三方陣になる。そこでこの魔方陣を「洛書(らくしょ)」とよんでいる。夏王朝の存在がまだ確認されていないうえ、この話の真偽もさだかではないが、すべてが事実だとすれば、約4000年前のことになる。このことはあいまいとしているが、少なくとも中国では2000年前には三方陣が存在していたと考えても間違いないようである。
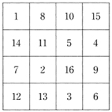
魔方陣は、現在では数学パズルの対象でしかないが、昔の人にはよほど神秘的なものに映ったらしく、中国ではこれを基に九星術という占いがつくられた。また、アラビアやインドでも、魔方陣を御守りや魔除(まよ)けに使っていた。西洋でも、その人の星座と魔方陣とを刻んだメダルを御守りに用いたことがある。は、ドイツの著名な画家デューラーの『メランコリー』と題する銅版画のなかに描かれている四方陣も占星術的な意味があると解釈される。なお、この魔方陣のいちばん下の段には、製作年度の1514が示されている(太字で示す)。
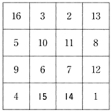
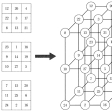
魔方陣のなかには、いろいろな特色をもつものがある。は完全方陣とよばれるものである。この魔方陣を横または縦方向に筒形に丸めて、上下または左右の辺を重ねると、それぞれ4本ずつ、計8本の対角線が生じるが、完全方陣ではこれらの対角線の数の和もすべて等しくなる。たとえば、
8+5+9+12=34
8+14+9+3=34
したがって、完全方陣の最上段を最下段の下に移す操作を順に行っていっても、すべて魔方陣となる。また、最左行を最右行の右に移す操作を順に行っても、やはり魔方陣になる。なお完全方陣のことを超魔方陣、ナシク方陣などとよぶこともある。
次に親子方陣というのはのようなもので、この十方陣ではぞれぞれの太線の中が魔方陣として成り立つ。つまりこの方陣は、十方陣であると同時に、八方陣でも、六方陣でも、四方陣でもあることになる。
これまで紹介したものは、いずれも平面の魔方陣であった。これに対して、立体の魔方陣も考えられる。それが立体方陣である。平面の場合、1からn2までの数を素材としているが、立体の場合は1からn3までの数が素材となる。立体方陣は、厳密にいえば縦、横、上下、平面対角線(斜め)、立体対角線のことごとくが等しくなくてはならないわけであるが、普通は平面対角線はかならずしも等しくなくてもよいことにしている。でも
縦 8+22+12=27+14+1=42など
横 8+13+21=9+14+19=42など
上下 8+10+24=3+14+25=42など
立体対角線 12+14+16=4+14+24=42
8+14+20=21+14+7=42
はすべて等しくなるが、平面対角線はそうとは限らない。
こうした立体方陣を最初につくったのは、有名な数学者フェルマーである。フェルマーは1640年に立体四方陣をつくっている。しかしこの作品では立体対角線が成り立たない。立体対角線も成立する立体四方陣を最初につくったのは久留島義太(くるしまよしひろ)である。
こうした1からn2まで、また1からn3までの数を素材とした魔方陣以外にも、多くの魔方陣がつくられている。そのなかでも、素数のみを素材にした素数方陣は、1900年にイギリスの数学パズル研究家H・E・デュードニー(1857―1930)が論じて以来、多くの人が研究している。はその一例である。
[高木茂男]
『平山諦・阿部楽方著『方陣の研究』(1983・大阪教育図書)』
百科事典マイペディア 「魔方陣」の意味・わかりやすい解説
魔方陣【まほうじん】
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「魔方陣」の意味・わかりやすい解説
魔方陣
まほうじん
magic square
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...