有理形関数（読み）ゆうりけいかんすう（英語表記）meromorphic function

日本大百科全書(ニッポニカ)

有理形関数
ゆうりけいかんすう
meromorphic function

複素数zを変数とする二つの多項式P(z),Q(z)が共通因数をもたないとき、f(z)=P(z)の形の関数を有理関数という。このとき、f(z)の特異点はQ(z)=0となるzだけである。そのようなzの一つをaとすると、
　　Q(z)=(z-a)^m(z),　(a)≠0
と書ける（このとき、aはm位のゼロ点であるという）。よってaの近くでは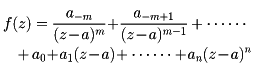

の形で書ける。

　関数f(z)が、aを中心とする半径Rの円内で、aを除いて正則なとき、aを孤立特異点という。このとき、0＜|z-a|＜Rを満足するzについて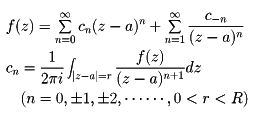

と展開できる。これをローラン展開という。とくに、c_-n(n＞0)のうち、0でない最大のnをpとするとき、aをp位の極であるという。無限遠点を除いた全複素平面で極以外の特異点をもたない関数を有理形関数という。

　有理関数は、無限遠点を含めた全複素平面で、極以外の特異点をもたないものとして特性づけられる。しかし、tanzなどのように有理関数でない有理形関数もある。

［洲之内治男］

偏角の原理

ある領域で極以外の特異点をもたない関数f(z)のm₁,m₂,……,m_p位のゼロ点をa₁,a₂,……,a_pとし、n₁,n₂,……,n_q位の極をc₁,c₂,……,c_qとする。このときこれらのゼロ点および極のすべてを内部に含むように正の方向（反時計回り）に一周する閉曲線Cに対して、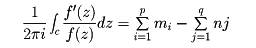

が成り立つ。これを偏角の原理という。この定理の応用として、代数方程式の根の存在定理などが説明される。

［洲之内治男］

[参照項目] | 関数論

出典　小学館　日本大百科全書(ニッポニカ)