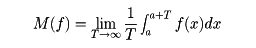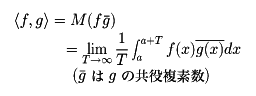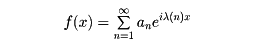概周期関数（読み）がいしゅうきかんすう（英語表記）almost periodic function

改訂新版　世界大百科事典

概周期関数 (がいしゅうきかんすう)
almost periodic function

概周期関数の理論は，1924年にボーアH.Bohrによって展開されたもので，周期関数の概念の拡張とみなされる。ボーアによる概周期関数の定義は次のとおり。

　すなわち，数直線上で定義された複素数値連続関数fについて，正の数εに対して，｜f（x＋τ）－f（x）｜≦εがすべてのxに対して成り立つような定数τのことを，εに属するfの概周期という。任意の正数εに対して適当な正の数lεを選ぶと，数直線上で長さlεの区間をどのようにとっても，εに属する概周期がその区間に含まれているならば，fを概周期関数という。

　連続関数fが周期wをもてば，任意のεに対して｜w｜より大きい数lは上記のlεの役目をするから，連続な周期関数は概周期関数である。その逆は成り立たない。例えば，sinx，sin\(\sqrt{2}\)xはそれぞれ2π，\(\sqrt{2}\)πを周期とする周期関数であるが，sinx＋sin\(\sqrt{2}\)xは周期関数でない。しかしsinx＋sin\(\sqrt{2}\)xは概周期関数である。

　一般に，f（x），g（x）が概周期関数で，cを定数とすると，f（x），cf（x），f（x）±g（x），f（x）g（x）は概周期関数である。また，概周期関数の列｛f_n｝が－∞＜x＜∞において一様にある関数fに収束すれば，fも概周期関数である。とくに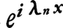（iは虚数単位）は周期関数，したがって概周期関数であるから，それらの一次結合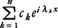（指数多項式という）も概周期関数であり，したがって指数多項式の列の一様収束極限の関数も概周期関数である。逆に，任意の概周期関数は指数多項式の列の一様収束極限である。

　任意の概周期関数f（x）に対して，平均と呼ばれる値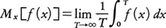，が存在する。a（λ）＝M_x［f（x）e⁻^iλx］とおくと，各f（x）に対してa（λ）≠0なるλはたかだか可算無限個しかない。それらをλ₁，λ₂，……，λ_n，……とし，a_n＝a（λ_n）とするとき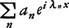，をfの（広義の）フーリエ級数という。これはふつうのフーリエ級数と類似の性質をもっている。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

概周期関数
がいしゅうきかんすう

1924年、オランダのボーアが周期関数の拡張として導入した関数。実軸上の複素関数f(x)が周期ωをもつとは、f(x＋ω)＝f(x)がすべてのxで成り立つことである。この拡張として、正の数εに対し、
　　|f(x＋τ)－f(x)|＜ε
がすべてのxで成り立つとき、τをεに属するf(x)の概周期という。連続関数f(x)が概周期関数とは、任意のε＞0を与えたとき、正の数L_εが決まり、長さL_εの任意の区間が、εに属する概周期を含むことで定義する。周期ωの周期関数は概周期関数の特別な場合であることは、ωがε＝0のときの概周期であることと、L₀をωにとればわかる。

　概周期関数f(x)に対し、その平均値

が決まり、しかも、この値はaのとり方に無関係である。また、e^iλx＝cosλx＋isinλxとすると、
　　M(e^iλx)＝1　(λ＝0);
　　M(e^iλx)＝0　(λ≠0)
だから、関数族｛e^iλx;－∞＜λ＜∞｝は内積を

で定義すると、この内積に関し正規直交系となり、概周期関数f(x)に対し、
　　a(λ)＝〈f,e^iλx〉
　　　　 ＝M(f(x)e^-iλx)
と置くと、a(λ)≠0となるλは、たかだか可算個であり、それをλ(1),λ(2),……とし、a_n＝a(λ(n))とすると、

と展開できる。これは周期関数のフーリエ級数の拡張となっている。

［洲之内治男］

[参照項目] | 周期関数

出典　小学館　日本大百科全書(ニッポニカ)