母関数（読み）ぼかんすう（その他表記）generating function

日本大百科全書(ニッポニカ)

母関数
ぼかんすう
generating function

数列a₀,a₁,……,a_nに対しtの関数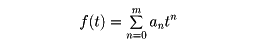

をその母関数という。たとえば(1+t)^mは二項係数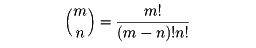

の母関数である。同様に無限数列a_nや関数列f_n(x)に対し、それぞれ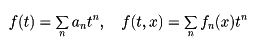

をその母関数という。また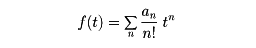

を数列a_nの指数的母関数といい、関数列についても同様である。

　応用上重要な母関数としては、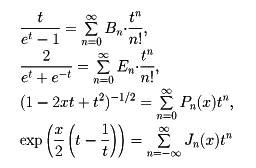

などがある。B_n,E_nはそれぞれベルヌーイ数、オイラー数であり、P_n(x),J_n(x)はそれぞれルジャンドルの多項式、ベッセル関数である。母関数が知られていれば、数列や関数列の積分表示を与えることができる。たとえば、関数列f_n(x)について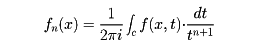

が成り立つ。ここで積分は複素積分で、Cは原点を中心とする正の向きの十分小さな円周である。また、母関数を用いて数列や関数列の間の関係が簡明に求まることがある。たとえばベルヌーイ数について、その母関数から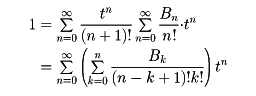

だから、両辺に(n+1)!を掛けてtⁿの係数を比較することにより、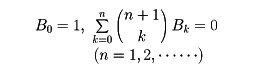

という関係式を得る。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

母関数 (ぼかんすう)
generating function

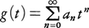生成関数ともいう。べき級数と数列｛a_n｝は1対1に対応する。g（t）を数列｛a_n｝に対する母関数という。数列｛a_n｝の諸性質を直接議論するかわりに母関数を用いると簡明であることが多い。より一般に，関数列｛f_n（x）｝に対し，ある変域のx，tに対して収束する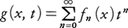を母関数という。母関数はラプラス変換やフーリエ変換として定義することが多い。母関数のうちでとくに確率変数xの関数θ^xの期待値でθ＝e^tとしたものは積率母関数，θ＝e^it（iは虚数単位）としたものは特性関数という。積率母関数M（t）＝E（e^tx）をtで偏微分した後t＝0と置くとE（x）となり，確率変数xの期待値が得られる。M（t）から，この偏微分操作によって，次々とxの高次モーメントを生成することができる。特性関数についても同様である。M（t）の自然対数はキュムラント母関数という。離散型分布ではθ＝tの場合である確率母関数P（t）＝E（t^x）がよく用いられる。これらは確率変数の漸近的性質などを調べるのにとくに便利である。なお，大文字E（ ・ ）は ・ の期待値をとることを意味する。
執筆者：広津 千尋

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

母関数
ぼかんすう
generating function

べき級数 y(t)＝Σa_ntⁿ を与えれば，数列 {a_n} が定まる。この場合 y(t) を，数列 {a_n} に対する母関数という。

出典　ブリタニカ国際大百科事典 小項目事典