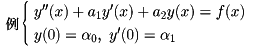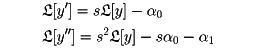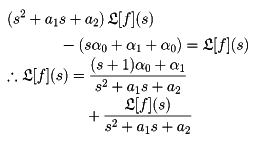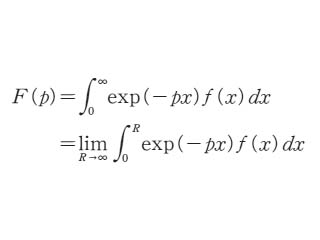改訂新版 世界大百科事典 「ラプラス変換」の意味・わかりやすい解説
ラプラス変換 (ラプラスへんかん)
Laplace transform
f(t)が区間(0,∞)で定義された関数であって,有限個の点を除いて連続であり,任意の有界な区間で有界変動であるとする。sを複素数として,積分,
を考えると,次のような定数σが定まる。
σ<∞のとき,半平面Re s>σにおいて正則な関数,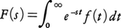
が定義される。この関数Fをfのラプラス変換という。関数の対応f Fもラプラス変換と呼ばれる。積分(1)が収束しても,積分,
Fもラプラス変換と呼ばれる。積分(1)が収束しても,積分,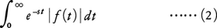
が収束するとは限らない。Re s=c(c>σ,c>0)において(2)が絶対収束するとき,F(s)からf(t)を求める反転公式,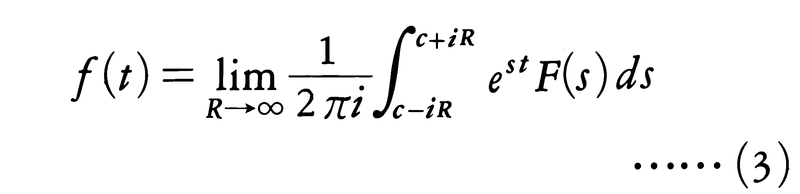
が成立する。ただし(3)の積分は,複素平面上の直線Re s=cの上でIm sの増加する向きに積分することを意味し,またfの不連続点aおよび0ではfを次のように修正する。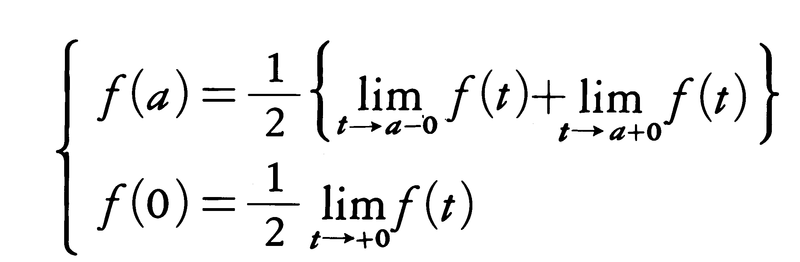
f,gが(0,∞)で定義されているとき,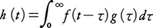
で定義される関数hをfとgのたたみ込み(または合成積)といい,f*gで表す。f,g,f*gのラプラス変換をそれぞれF,G,Hとするとき,fとgに対する(2)の積分が収束すればF(s)G(s)=H(s)が成り立つ。
ラプラス変換の例としていくつかあげる。fのラプラス変換がFであることをf Fと書くことにすると,
Fと書くことにすると,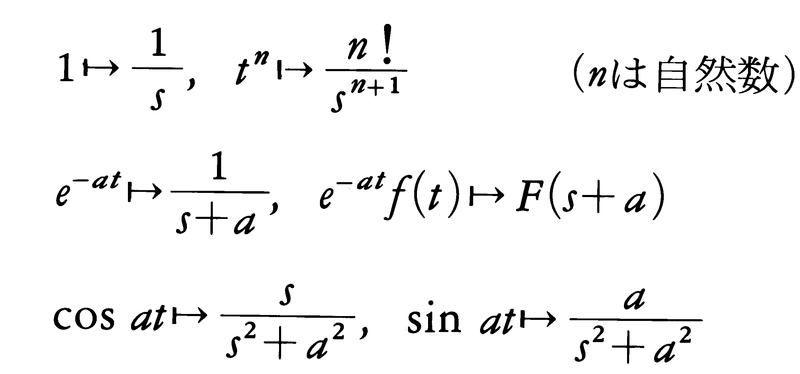
である。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


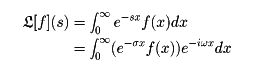
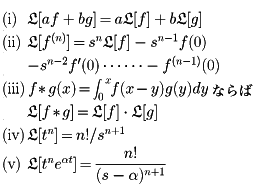
 [f](s)の表がつくられている。その使い方を例で示す。
[f](s)の表がつくられている。その使い方を例で示す。