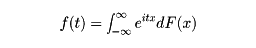特性関数 (とくせいかんすう)
characteristic function
確率分布や確率変数に対して定まる一つの関数であり,初めレビP.Lévyによって導入され,確率分布の性質や確率変数列の極限などを調べるのに役だってきた。直線上の分布関数F(x)の特性関数φ(t)はスティルチェス積分,
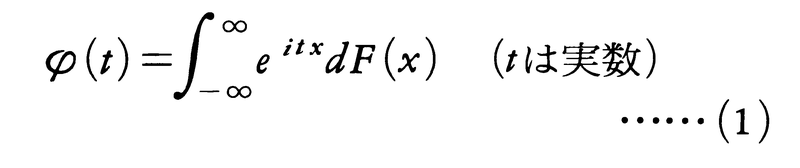
で与えられ,次の3性質をもつ。(1)tについて連続,(2)正定値,すなわちどんな有限個のt1,t2,……,tnと複素数α1,α2,……,αnに対しても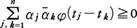 ,(3)φ(0)=1。逆に,(1)~(3)を満たす関数φ(t)があれば,(1)の関係にある分布関数F(x)がただ一つ定まる。これをボホナーS.Bochnerの定理という。
,(3)φ(0)=1。逆に,(1)~(3)を満たす関数φ(t)があれば,(1)の関係にある分布関数F(x)がただ一つ定まる。これをボホナーS.Bochnerの定理という。
確率変数Xについては,その分布関数の特性関数をXの特性関数という。それは,
φ(t)=E(eitx) ……(2)
と表される。X1,X2が独立であるとき,それらの特性関数をφ1(t),φ2(t)とすれば,和X1+X2には積φ1(t)・φ2(t)が特性関数として対応する。特性関数の列がある特性関数に収束するとき対応する分布の収束が保証されるなど,確率統計の議論で重要な役割を果たしている。
特性関数の例としては,(1)二項分布{b(k;n,p)}:(peit+q)n,(2)ガウス分布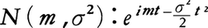 ,(3)ポアソン分布
,(3)ポアソン分布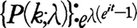 ,(4)自由度nのχ2-分布:(1-2it)⁻n/2などがある。
,(4)自由度nのχ2-分布:(1-2it)⁻n/2などがある。
多次元分布やベクトル値をとる確率変数の場合の特性関数も同様に議論できる。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
特性関数
とくせいかんすう
確率変数Xの分布関数をF(x)とする。すなわちF(x)=P(X<x)とする。このとき
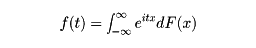
を確率変数Xの特性関数という。確率変数Xの特性関数をf(t)、確率変数Yの特性関数をg(t)とする。X、Yが独立な確率変数であれば、X+Yの特性関数はf(t)・g(t)で与えられる。
特性関数は分布関数によって決まる。二項分布B(n,p)の特性関数は(peit+q)n、ポアソン分布P(λ)の特性関数はexp(λeit-1)、正規分布N(m,σ2)の特性関数はexp(imt-(σ2/2)t2)である。
[古屋 茂]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
特性関数
とくせいかんすう
characteristic function
(1) 確率論で確率変数の分布の特性を示す関数で,確率密度のフーリエ変換をいう。 (2) 一般に集合 Xの部分集合 Aに対し,Aを指定するために x∈Aなら1,x∉Aなら0として,xが Aに入るかどうかを判断すればよいが,これを X上の関数と考えて Aの特性関数という。これについては特徴関数,定義関数などの用語も使われる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内の特性関数の言及
【ゲーム理論】より
… また同一のゲームが反復して行われる反復ゲーム,ある部分ゲームから他の部分ゲームに確率的に移行する確率ゲーム,ゲームの状態や戦略が連続な時間の関数として表される微分ゲームなどのように,時間の経過に伴って行われるさまざまな多段階ゲームがある。(3)提携型または特性関数型 協力ゲームの表現方法で,n人のプレーヤーのうち何人かが提携して,その提携内では合意によってとるべき戦略が決定され,提携としてのとりうる値(提携値)が定まるような状況を示すものである。各提携に対して,その提携値を与える関数を特性関数と呼ぶ。…
【母関数】より
…母関数はラプラス変換やフーリエ変換として定義することが多い。母関数のうちでとくに確率変数xの関数θxの期待値でθ=etとしたものは積率母関数,θ=eit(iは虚数単位)としたものは特性関数という。積率母関数M(t)=E(etx)をtで偏微分した後t=0と置くとE(x)となり,確率変数xの期待値が得られる。…
※「特性関数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
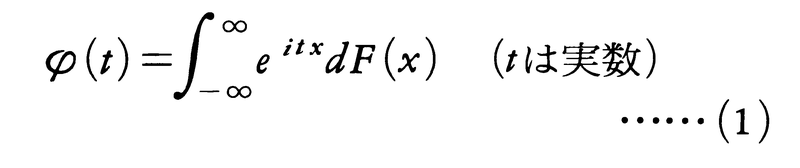
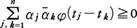 ,(3)φ(0)=1。逆に,(1)~(3)を満たす関数φ(t)があれば,(1)の関係にある分布関数F(x)がただ一つ定まる。これをボホナーS.Bochnerの定理という。
,(3)φ(0)=1。逆に,(1)~(3)を満たす関数φ(t)があれば,(1)の関係にある分布関数F(x)がただ一つ定まる。これをボホナーS.Bochnerの定理という。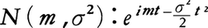 ,(3)ポアソン分布
,(3)ポアソン分布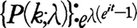 ,(4)自由度nのχ2-分布:(1-2it)⁻n/2などがある。
,(4)自由度nのχ2-分布:(1-2it)⁻n/2などがある。