相乗平均（読み）ソウジョウヘイキン（その他表記）geometric mean

デジタル大辞泉

そうじょう‐へいきん〔サウジヨウ‐〕【相乗平均】

n個の数値があるとき、それらを全部掛け合わせた積のn乗根。幾何平均。

出典　小学館

精選版 日本国語大辞典

そうじょう‐へいきんサウジョウ‥【相乗平均】

1. 〘 名詞 〙 平均値の一つ。ｎ個の正数の相乗積のｎ乗根を、それらの数の相乗平均という。幾何平均。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

相乗平均 (そうじょうへいきん)
geometric mean

幾何平均ともいう。n個の正数x₁，x₂，……，x_nがあるとき，これらの数の積のn乗根をx₁，x₂，……，x_nの相乗平均という。相乗平均は変動率などを平均するのに適している。例えば，元金がAで，第1年目，第2年目，……，第n年目の年利率がそれぞれr₁，r₂，……，r_nであるとき，平均年利率をrとすると，どちらの方法でもn年後の元利合計が同じであるから，A（1＋r₁）（1＋r₂）……（1＋r_n）＝A（1＋r）ⁿとなり，元金の変動率 1＋rは 1＋r₁，1＋r₂，……，1＋r_nの相乗平均である。また平均年利率rは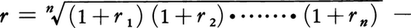，である。n個の正数x₁，x₂，……，x_nの相乗平均は，これらの数の相加平均（x₁＋x₂＋……＋x_n）/nより大きくない。二つの平均が等しくなるのはx₁＝x₂＝……＝x_nとなる場合だけである。
執筆者：野本 久夫

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

相乗平均
そうじょうへいきん

n個の正数a₁,a₂,……,a_nに対して、これらn個の数の積のn乗根

をa₁,a₂,……,a_nの相乗平均または幾何平均という。相乗平均はa_i(i=1,2,……,n)がすべて正数のときに限って定義されるものであることに注意しなければならない。相乗平均は物価指数などの指数や所得分布の代表値として用いられる。

　a₁,a₂,……,a_nが正数のとき、これらの相加平均、相乗平均、調和平均をそれぞれA、G、Hで表すと
　　H≦G≦A
が成り立つ。ここでH=Gであればa₁=a₂=……=a_nであり、G=Aであればa₁=a₂=……=a_nである。また、正数a_i(1≦i≦n)の相乗平均をGとするとlogGはloga_iの相加平均になっている。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

相乗平均【そうじょうへいきん】

幾何平均とも。n個の正数a₁，a₂，…，a(/n)の積のn乗根，つまり（式１）。相乗平均は相加平均に等しい（a₁＝a₂＝…＝a(/n)のとき，そのときに限る）かそれより小さい。
→関連項目調和平均｜平均

出典　株式会社平凡社

栄養・生化学辞典

相乗平均

　幾何平均ともいう．平均しようとする値をすべてかけ合わせてその結果をかけた項目の数で開いた平均．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

相乗平均
そうじょうへいきん

「幾何平均」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の相乗平均の言及

【平均】より

…確率変数Xの平均(期待値)E(X)は(4)の形で数学的に定義される。　n個の正の実数x₁,x₂，……，x_nに対して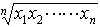，を相乗平均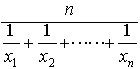，を調和平均という。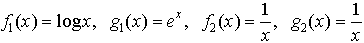とすると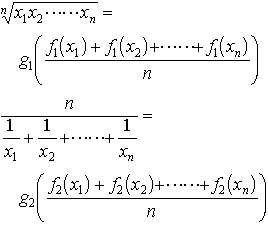，となっている。…

※「相乗平均」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」