日本大百科全書(ニッポニカ) 「誘導形」の意味・わかりやすい解説
誘導形
ゆうどうけい
reduced form
計量経済学において、一連の連立方程式体系として設定されたモデルを、そのなかの内生変数について解くことによって、各内生変数の変動を先決変数(外生変数および先決内生変数)のみで表す関係式に変形したもの。
いま、経済の構造を、国民所得Yと消費支出Cの二つの内生変数を中心とし、それに投資Iを外生変数として導入することによって、次の方程式体系によって表すものとする(uは確率的な変動部分を表す)。
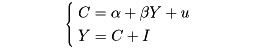
これが一つの(もっとも簡単な)計量経済モデルである。この連立方程式を内生変数CとYについて解いたもの、すなわち、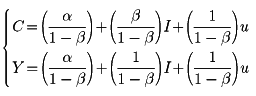
が、先のモデルから導かれた誘導形である。
誘導形は、二つの目的から必要とされる。一つは、構造方程式のパラメーターαおよびβを統計的に推定する際に用いられる。α、βを元の方程式について直接推定しようとすると、変数Yと確率項uとが相互に依存関係をもつために、それらの推定値は真の値から偏りのあるものとなる。そのために、誘導形を導くことによって、各内生変数を外生変数と確率項だけによって書き換え、そのような相互依存関係を取り除いたうえでパラメーターを推定する。こうすることによって偏りのない推定値が得られるが、それは誘導形のパラメーターであり、そこから元のパラメーターα、βを求める。しかし、このように誘導形パラメーターから元のパラメーターがつねに一定の値として得られるとは限らない。
誘導形のもう一つの目的は、経済分析に関するものである。たとえば、先のYについての誘導形方程式をみると、誘導形パラメーター(あるいは元のパラメーターβ)が統計データから推定されていれば、経済社会全体の投資額がかりに1兆円増加したとすれば、国民所得はその1/(1-β)倍だけ増大することがわかる。また、Cについての誘導形方程式からも同様のことが具体的な数量関係として得られる。このようにして、誘導形を経済政策の立案や経済構造の分析に役だてることができる。
[高島 忠]

