日本大百科全書(ニッポニカ) 「構造方程式」の意味・わかりやすい解説
構造方程式
こうぞうほうていしき
structural equation
計量経済学においては経済活動の因果関係を方程式として表現するが、それがある特定の経済社会や経済行動の基本構造を示すものとして実際の観測データから具体的に推計されたとき、それを構造方程式とよぶ。
いま、国民経済全体の活動の姿を次のような方程式の体系として表現したとする。
Ct＝a0＋a1Yt＋a2Ct-1＋ut…(1)
Yt＝Ct＋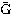
t……………(2)
ここで、Yは国民所得、Cは国民全体としての消費額、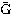は国民経済としての消費以外の最終需要、すなわち投資や政府支出などの額を表す。これらの各変数の右下についているtは期間を意味し、したがってCt-1は1期間前の消費額を示している。(1)式の右辺の各変数の前に置かれたa0、a1、a2は、t期の消費額Ctとその動きを説明する変数Yt、Ct-1とを結び付ける定数または係数である。また、同じ式の右辺の最後に置かれたutは、採用された説明変数の動きによっては説明されえない部分を説明するために、それが人間行動の不確実性に基づくものであると考えて導入されたものであり、確率攪乱(かくらん)項とよばれる。このように、経済活動の因果関係を一般的な方程式体系として表現したとき、それは経済の「モデル」とよばれる。そして、それは経済理論や統計的関係に基づいて構築される。
このようにして構築されたモデルを用いて、ある特定の経済活動が具体的にどのような数量的因果関係に基づいて構成されているのかをみいだすことが、計量経済学的研究の基本的な仕事となる。その作業は、モデルに採用された経済変数のそれぞれの動きを、実際の観測データ（統計数字）を用いて追うことによって行われる。それらのデータに基づいて、研究対象としている経済活動の具体的な構造を表すものとして、経済変数間の数量的因果関係を規定する定数あるいは係数（これらはパラメーターとよばれる）が推定されるわけである。たとえば、先に示したもっとも簡単な国民経済のモデルを、日本経済の1970年（昭和45）から1989年（平成1）までの20年間のデータを用いて推定した結果は、次のようになったとしよう。
Ct＝77.5＋0.253Yt＋0.656Ct-1 …(3)
Yt＝Ct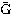＋t………………………(4)
これが日本経済の当該期間に関する基本構造を表す方程式の体系であり、これを「構造方程式体系」とよぶ。そして、これを構成するおのおのの方程式が推定された「構造方程式」である。もし、1990年以降のデータを用いて同じモデルを推定したとしたならば、おそらく各係数の値は異なったものとなるであろう。そういう結果が出たとするならば、日本経済はバブル崩壊後の「失われた十年」とそれに続く金融危機・世界同時不況という20年の経過のなかで、はっきりと「構造」変動をおこしたことが、計量経済学的に明らかにされることになる。
構造方程式は、それが表す数量的関係の性質によって、一般に「行動方程式」と「定義式」とに分けられる。前者は人間のある種の経済行動を数量的因果関係として表したものであり、後者は単に経済変量間の統計上の定まった関連を示すものである。先に例示した構造方程式体系についていえば、(1)または(3)式が行動方程式であり、(2)または(4)式が定義式である。
［高島 忠］