日本大百科全書(ニッポニカ) 「識別問題」の意味・わかりやすい解説
識別問題
しきべつもんだい
identification problem
計量経済学において、相互依存の関係にある経済変数間の変動のようすを一連の方程式体系として数量的に表現し、実際のデータを観測することによってそれらを生み出す具体的な構造を推定しようとする際、想定された各方程式が観測データの背後にある正しい構造を表すものとしてみいだすことができるかどうかの問題。アイデンティフィケーションの問題、認定問題ともよばれる。
[高島 忠]
識別可能性
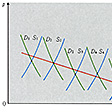
いま、ある商品について、その価格pと需要量qに関して何か年かにわたるデータを調べたところ、価格の低下(あるいは需要量の増大)につれて需要量が増大(あるいは価格が低下)してきたとしよう。このようすを(p、q)の点としてグラフ上に描くと、点の動き方は右下がりとなる。したがって、この観測データは、この製品に関する消費者の需要行動を表すものとして、これから需要関数を導くことができるように思われるが、実はそうではない。なぜならば、市場において実際に観測された各点(p、q)は取引価格pと取引数量qとの関係を示すのであって、qは需要量を示すとともに供給量をも示すものだからである。すなわち、観測された各点は、各観測時における需要曲線Dと供給曲線Sとの交点を表すものであって、真の需要曲線(および供給曲線)は、のように観測値の背後に存在するのである。したがって、需要関数をp、qの関係式(たとえばq=α+βp)として表し、以上の観測データに基づいてその式を推定(α、βの値を定める)しても、それは一般には、真の需要関数を示すものとはならない。この商品市場の動きを一つの方程式体系(モデル)によって示すと、次のようになる。
(1) qD=a0+a1p+a2x
(2) qS=b0+b1p+b2y
(3) qD=qS
第1式は需要関数、第2式は供給関数であり、第3式は、各時点での両関数による曲線の交点として取引量が決定されることを示している。xは所得水準や消費者の嗜好(しこう)などを表し、これは、需要曲線をD1、D2、D3、……のようにp‐q図表上で移動させる要因となる。これに対してyは供給者側の条件変動を表すものであり、生産設備量とか生産量などの要因が考えられる。そのような要因yが変化することによって、供給曲線はp‐q図表上でS1、S2、S3、……と変位するわけである。
いま、xの係数a2が0であり、需要曲線を変位させる要因が存在しなかったとするならば、需要曲線はp‐q図表上でD1のままであるから、供給曲線Dの変位に伴って観測点はD1線の上に並ぶ。すなわち、この場合には、観測データの集合から需要曲線は判明するが、供給曲線はみいだしえない。このような状況にあるとき、需要に関する構造方程式(1)は「識別(認定)可能」であるが、供給に関する構造方程式(2)は「識別(認定)不能」であるといわれる。需要曲線のかわりに供給曲線を変位させる要因yが存在しない場合には逆の結果となる。また、xとyの両要因が存在し、これらが同じ要因であるか、互いに関連をもって動くような場合には、両構造方程式とも識別不能となるのに対して、xとyが個々に独立に動く要因(外生変数とよばれる)の場合には、両構造方程式とも識別可能となる。その理由は、前者の場合には両構造が観測データの背後にまったく隠されてしまうのに対して、後者の場合には一方の構造の外的要因が動かない間に他方の構造の外的要因が変動することが可能だからである。
[高島 忠]
識別可能条件
識別可能性の問題を一般的に考察する場合、それは、経済モデルである連立方程式体系を誘導形に解いた(内生変数について解いた)とき、その誘導形パラメータから各構造方程式のパラメータが単一のものとして定まるかという問題に翻訳される。この問題を検討することによって導かれる一つの識別可能性の条件は、次のようなものである。G本の構造方程式からなる経済モデルにおいて、そのなかのある構造方程式が識別可能であるためには、他の方程式のいずれかには採用されていてその方程式には採用されていない変数の数がGマイナス1以上でなければならない。一般に、その数がGマイナス1より少ない場合は「過小識別」とよばれ、識別不能である。Gマイナス1に等しい場合は「適度識別」、Gマイナス1より多い場合は「過剰識別」といわれる。この判別条件は「次数条件」とよばれる一つの必要条件であり、識別可能なための必要十分条件としては、別に「階位条件」とよばれるものが一般的な形で求められている。
[高島 忠]