関連語
改訂新版 世界大百科事典 「オイラーの多面体定理」の意味・わかりやすい解説
オイラーの多面体定理 (オイラーのためんたいていり)
Euler's theorem on polyhedra
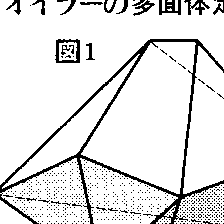
表面がいくつかの多角形の面からなっている立体を多面体という。とくに,多面体の面を含む平面がこの面以外では多面体と交わらないようなものを凸多面体という。一つの多面体において,その頂点の個数をα0,辺の個数をα1,面の個数をα2とするとき,α0-α1+α2をその多面体のオイラー標数(種数)という。凸多面体ではオイラー標数はつねに2になる(図1)。L.オイラーによって1752年に発見されたこの定理は位相幾何学における最初の重要な成果で,オイラーの多面体定理と呼ばれている。この結果はすでにR.デカルトによっても得られていたと伝えられている。凸多面体でない多面体でも,その表面を連続的に変形して球面にすることができるときには,オイラー標数はやはり2となる。しかしながら,図2のような〈穴〉が一つある多面体ではオイラー標数は0となる。一般に,〈穴〉がp個ある多面体ではオイラー標数は2(1-p)となる。なお,オイラーの多面体定理より正多面体はたかだか5種類しか存在しないことが容易に示される。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
法則の辞典 「オイラーの多面体定理」の解説
オイラーの多面体定理【Euler's polyhedron theorem】
F+V=E+2
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...