演算子法（読み）エンザンシホウ（英語表記）operational calculus

デジタル大辞泉

えんざんし‐ほう〔‐ハフ〕【演算子法】

演算子を用いて、ある演算を行う方法。例えば、微分の演算を、記号d/dtを用いて微分方程式で解く方法。

出典　小学館

精選版 日本国語大辞典

えんざんし‐ほう‥ハフ【演算子法】

1. 〘 名詞 〙 演算子間の一種の算法。これにより、微分、積分などの複雑な計算を代数的、機械的に行なうことができる。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

演算子法 (えんざんしほう)
operational calculus

関数に対する微分や積分の演算を記号的，あるいは代数的に行い，微分方程式を形式的に解く手法を演算子法という。19世紀の終りころに，イギリスの工学者O.ヘビサイドが電気工学におけるいろいろな現象を記述する常微分方程式や，電信方程式と呼ばれる偏微分方程式を解くのにこの手法で成功をおさめて以来，演算子法はまとまった一つの理論となった。しかし，彼の議論は数学の対象としうるほどの厳密さを備えていなかった。その後，ラプラス変換や超関数などによる裏づけがなされてしだいに体系を整えてきた。なかでも，1951年にポーランドのJ.ミクシンスキが《演算子法》（1963-64邦訳）を著して明快で厳密な基礎づけを行った功績は大きく，以後，数学の一分野となった。

　ミクシンスキの方法はラプラス変換を直接援用しないですむこと，超関数と基本的なところでつながっていることなどの特徴があり，今日のような発展の基礎となった。その理論の出発点は，t≧0で定義された二つの連続関数a（t），b（t）の合成積である。それは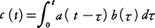，で定まる連続関数c（t）のことで，c＝a・bとかく。この演算は通常の掛算と同様な性質をもっている。とくにcが恒等的に0に等しい関数であったとすれば，aかbのいずれかが恒等的に0に等しい。以後，関数はt＜0では恒等的に0として直線全体で定義されているとしたほうが好つごうである。このとき，数の掛算でいえば1にあたる関数はもはやふつうの関数ではなくて，P.A.M.ディラックのデルタ関数δ（t）である。それは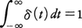であるが，0を含まない区間I上では，いつも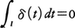となるべきもので，超関数として初めて正当化される。そして，すべてのaに対してa・δ＝aである。また割算a/bも定義される。例えばt≧0で，a（t）＝t²，b（t）＝tならc（t）は同じくt≧0で恒等的に2となる関数である。それは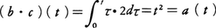から知られる。こうして割算も考えることができて，商体，すなわちa/bのように表されるもの全体（正確にはそれらの同値類）が定義される。その商体の要素を演算子と呼ぶ。

　関数aの積分をl・aとかく。

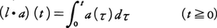このときlは（l・a）/aで一つの演算子となる。lの逆元s＝1/lが微分演算子である。例えばa（t）が導関数a′（t）をもてば，sa＝a′＋a（0）となることがわかる。t＜0のとき0，t＞0のとき1（t＝0では1/2とすることが多いが，その値にこだわらない）である関数をヘビサイドの関数，あるいは単位関数といい，1あるいは1（t）とかく。これに対しては，s1＝δが成り立つ。lやsの多項式も演算子として定義され，それぞれ繰り返して積分したり，高階の導関数やその一次結合をとる操作を表す。さらにsの有理関数も微分方程式の形式的解法にあたって自然に導入され，その方程式の形式的解法を指示する。例えばx（t）についての微分方程式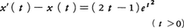，を初期条件x（0）＝2のもとで解こう。演算子を用いてかけば，x′（t）＝sx（t）－2に注意して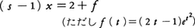，ゆえに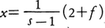となる。一般に\(\frac{1}{s－α}\)（αは定数）は関数e^αtに対応するので，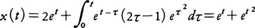

が得られる。電気工学の例として，L，C，Rの回路に起電力Eが働いている場合を考えよう。電流をI，コンデンサーの荷電をQとおけばLI′＋RI＋Q/C＝E，ただしQ′＝I（′は時間微分を表す）となるが，演算子を用いてかくと，コンデンサーの電圧をVとして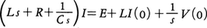，となる（V（0）＝－Q（0）/C）。これを解いて電流，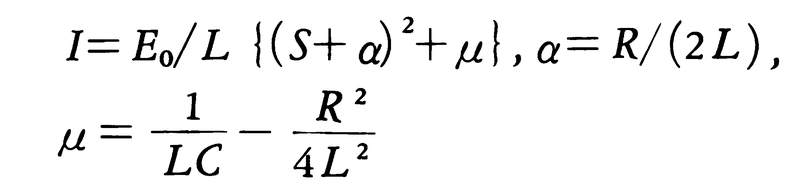

が求められる。ただしE₀はt＝0での起電力。

　ラプラス変換との関連は\(\frac{1}{s－α}\)が関数e^αtに対応することが鍵となる。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

演算子法
えんざんしほう

微分や積分を含む方程式を演算子（写像）の代数方程式とみなして解く方法をいう。たとえば、微分するという演算を記号化してDで表し、tの関数f(t)に対し、1階、2階、……m階の導関数をそれぞれ
　　Df＝f′(t),D²f＝f″(t),……,
　　　D^mf＝f^(m)(t),……,
とし、また、
　　D⁰f＝1・f＝f(t)
とすると、D^mDⁿ＝DⁿD^mとなり
　　p(D)＝Dⁿ＋a₁D^n-1＋……
　　　＋a_n-1D＋a_n
をつくると、これは加減乗法に関しては多項式と同様に計算できる。つまり、微分方程式
　　f′(t)＋af(t)＝h(t)
は(D＋a)f＝h(t)となる。したがって、割り算を適当に意味づけることができると、解は、
　　f(t)＝(D＋a)^-1h(t)
によって求められる。このように、微分方程式を代数的な計算で解こうという試みは古くからあったが、1890年代にイギリスの電気学者ヘビサイドが考案した方法を普通、演算子法とよんでいる。ヘビサイドの着想は巧妙であったが、ラプラス変換などを用いて数学的に厳密な正当性が示されたのは約50年後であった。

　ヘビサイドは、割り算として、微分と積分が互いに逆演算であることに着目し、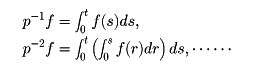

を定義し、演算子p^rをp^rp^-rf＝fとなるものとして定義した。pは微分演算子Dに相当するものであるが、その関係はg(t)＝f′(t)＝Dfと置くと、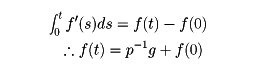

この両辺にpをほどこして、まとめると、
　　Df(t)＝pf(t)－pf(0)
同様にして、
　　D²f(t)＝p²f(t)－p²f(0)＋pf′(0)
　ヘビサイドは、このように定義したpをあたかも数のように取り扱い、pの関数とtの関数を対応させた。その対応は表になって与えられている。

　最近ミクシンスキーJ. G. Mikusinskiは次のような考えから演算子法に新しい解釈を与え、その応用を拡大したので、演算子法は面目を一新している。整数全体の集合Zは加減乗法ができるばかりでなく、ab＝0ならばaまたはbがゼロという性質から分数をつくり、除法が可能になったことをまず思い出そう。Zのかわりに、正の数xに対し定義された連続関数の全体をCで表し、Cの要素f、gに加減法をf(t)±g(t)で定義し、乗法を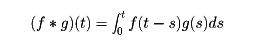

で定義すると、Zと同様に(f*g)(t)≡0ならばf(t)≡0またはg(t)≡0という性質をもつことがいえる（≡は、関数が恒等的にゼロに等しいことを示す）。よって、整数から分数をつくったのと同じ考えで、Cから「分数」に相当するものをつくると、積の逆演算が可能になる。二つの連続関数の「分数」をミクシンスキーの演算子という。なお、ヘビサイドの演算子はミクシンスキーの演算子の特別な場合になる。

［洲之内治男］

『ミクシンスキー著、松村英之・松浦重武・笠原皓司訳『演算子法』上下（1963・裳華房）』▽『吉田耕作著『演算子法』（1982・東京大学出版会）』

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

演算子法
えんざんしほう
operational calculus

普通には，微分演算，積分演算を記号的，代数的に行うことをいう。すなわち演算子となる記号
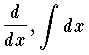を用いて演算すること，あるいは定数係数をもつ線形微分方程式を簡単に解くために，ヘビサイドの方法やラプラス変換を用いて演算する解法のことを演算子法という。 x のある関数 y の導関数 f'(x)＝dy/dx を求めるための微分演算は，d/dx を1つの文字 p で表わせば，関数 y に関数 py を対応させることであるから，p は1つの演算子と考えてよい。この p を微分演算子という。ある一定の規約のもとに，このような演算子 p₁ ，p₂ を代数的文字のように取扱って，演算子の間に和，差，積，累乗などを定義し，また数も1つの演算子と考えれば，定数係数の線形微分方程式は非常に容易に解ける。これがヘビサイドの演算子法といわれるものである。数学的により完全な基礎をもつ方法として，ラプラス変換を用いて微分方程式を解く方法がある。近年ポーランドのミクシンスキーは，関数の間にたたみこみ (接合積) を基礎にした厳密な裏づけを行い，吉田耕作はそれを簡易化した。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の演算子法の言及

【演算子法】より

…関数に対する微分や積分の演算を記号的，あるいは代数的に行い，微分方程式を形式的に解く手法を演算子法という。19世紀の終りころに，イギリスの工学者O.ヘビサイドが電気工学におけるいろいろな現象を記述する常微分方程式や，電信方程式と呼ばれる偏微分方程式を解くのにこの手法で成功をおさめて以来，演算子法はまとまった一つの理論となった。…

※「演算子法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」